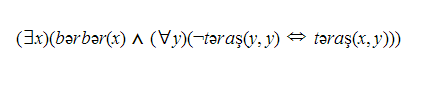Bərbər paradoksu
Bərbər paradoksu — Rassel paradoksundan yaradılmış tapmacadır. Bertran Rassel tərəfindən yaradımışdır. Bu paradoksu ona tövsiyə edən adsız bir kişiyə ithaf etmişdir.
Paradoks
[redaktə | mənbəni redaktə et]Sadəcə bir kişi bərbərin olduğu qəsəbə düşünün. Bu qəsəbədə hər kişi bunlardan birini etməklə daima taraşlı gəzməkdədir.
- özünü taraş edərək
- bərbərə gedərək
Fərqli şəkildə ifadə edərsək: bərbər yalnız qəsəbədə özünü taraş edə bilməyən kişiləri taraş edir. Bunlar aşağıdakı paradoksal sual xaricində məntiqli görünməkdədir.
- Bərbəri kim taraş edir?
Bu sual paradoks yaradır. Bərbər yalnız aşağıdakı adamlar tərəfindən taraş edilə bilər.
- özü
- bərbər (yenə özü)
Ancaq bu variantlardan heç biri keçərli deyil. Çünki:
- Əgər bu adam özünü taraş edərsə, bərbər (özü) tərəfindən taraş edilməməli.
- Əgər bu adam özünü taraş etməzsə, bərbər (özü) tərəfindən taraş edilməli.
Birinci dərəcə məntiqlə ifadəsi
[redaktə | mənbəni redaktə et]Paradoks yaratmayan alternativlər
[redaktə | mənbəni redaktə et]Bu paradoksun başqa formaları zaman-zaman məntiq sualı olmuşdur. Bu versiyada bərbər haqqında məlumat verilməməkdədir. Həlli isə bərbərin qadın (ya da uşaq, qorilla, başqa qəsəbədən bir kişi və ya kişi xaricində başqa bir şey) olmasıdır. Bu paradoks yaratmır. Bərbər paradoksunun yaranması üçün bərbərin "özünü taraş etməyən hər kəsi taraş etmə" iddiasının ozünü də əhatə etməsidir. Rassel paradoksu Kantorun standart çoxluqlar nəzəriyyəsindəki təməl boşluğu vurğulayır. Paradoksun əsas vurğuladığı sual belədir: çoxluq özünün alt çoxluğudurmu? Sual riyaziyyatı çoxluqlar nəzəriyyəsindən qurmaq istəyən riyaziyyatçılar üçün problem yaratmışdı. Məsələni Hilbert və digər dövrün məşhur riyaziyyatçıları müzakirə edib cavab verməyə çalışsalar da, dahi yəhudi əsilli avstriyalı filosof Ludviq Vittgenstayn 70 səhifəlik "Məntiqi fəlsəfi traktat" əsərində birdəfəlik həll etmişdir. Belə ki, çoxluq özünün alt çoxluğu deyildir. Paradoks bununla da öz həllini tapmışdır. Lakin buna baxmayaraq, hələ də çoxluq anlayışına dəqiq riyazi tərif vermək mümkün deyil.