Sonlu elementlər üsulu
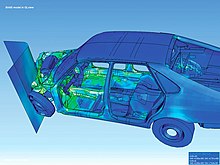
Sonlu elementlər üsulu (SEÜ)- tətbiqi fizikanın ədədi həll üsuludur. Deformasiya oluna bərk cism mexanikası, istilik mübadiləsi prosesləri, hidrodinmaika və elektrodinamikada bu üsuldan geniş istifadə olunur. Qoyulmuş çətin həll olunan texniki məslələrin həlli təqribi olaraq sərhəd şərtlərinə malik elliptik differensial tənliklərin köməyi ilə aparılır. Bu mühəndislikdə müasir hesablama üsullarından sayılır.
Üsulun mahiyyəti
[redaktə | mənbəni redaktə et]Hesablama riyaziyyatı baxımından sonlu elementlər üsulunun mahiyyəti ondan ibarətdir ki, məsələnin funskionallığının minimallaşdırılması ayrı-ayrılıqda alt sahələrdə müəyyən olunmuş funksiyalar toplusu kimi baxılır və sistemin ədədi anlaizi onu tam bir vahid kimi nəzərə alır.
Üsulun yaranma tarixi
[redaktə | mənbəni redaktə et]Sonlu elementlər üsulunun yaranması 1950-ci ildə kosmik məsələlərin həlli ilə bağlıdır. Bu üsul tikinti mexanikası və sərtlilik nəzəriyyəsindən məlum olmuş, sonralar isə onun riyazi əsası işlənmişdir. SEÜ əsas təkanı 1963-cü ildə tikinti mexanikasında potensial enerjinin minimallaşdırlması ilə sisitemin həllini tarazlığın xətti asılılıqları ilə əvəz olunmasına gətirilməsinin Reley-Rits üsulunda sübutundan sonra almışdır. SEÜ minimallaşdırma ilə əlaqəsini sübut edəndən sonra o Laplas və Puasson düsturları ilə ifadə olunan məsələlərə də tətbiq olunmağa başaldı. Getdikcə SEÜ geniş tətbiqi və onun riyazi əsasınn genişləndirilməsi bu üsulla çətin həll olunan differensial tənliklərin həllinə də şərait yaratmışdır.
Əsas konseptləri
[redaktə | mənbəni redaktə et]Bütün verilmiş fəzanın kiçik hissələrə bölünməsinin bir neçə üstünlükləri vardır:
- Kompleks geometriyanın dəqiq təmsil edilməsi
- Oxşar olmayan material xüsusiyyətlərinin özündə ehtiva edilməsi
- Toplam həllin asan təmsil edilməsi
- Lokal effektlərin təyini
Bu üsulun nümunəvi işinə (1) fəzanın, hər biri əsas problemdə elementlər bərabərlikləri ilə təmsil edilən kiçik altfəzalara bölünməsi və daha sonra (2) son hesablamada bütün element bərabərlikləri topluluqlarının sistematik olaraq bir yerə toplanması daxildir. Xətt cəbri tənliklərinin sistemi tərtib edilir. Bərabərliklərin qlobal sisteminin bilinən rəqəmsal həll üsulları vardır və original problemdə verilən ilkin dəyərlərə əsaslanmaqla həlli əldə edilir. Tənliklərin miqdarı ilkin sistemin həlli axtarılan düyünlərdə naməlum dəyərlərin miqdarına bərabərdir, elementlərin miqdarına düz mütənasibdir və yalnız EHM-in imkanlarıyla məhdudlaşdırılır. Elementlərdən hər biri məhdud sayda olan qonşu elementlərin miqdarıyla məhdudlaşdırıldığı üçün, xətti cəbr tənliklərinin sistemi seyrəldilmiş növə malikdir ki, bu onun da həllini əhəmiyyətli dərəcədə sadələşdirir.
Üsula əsaslanan analiz sistemləri
[redaktə | mənbəni redaktə et]SEÜ ilə işləyən ən geniş yayılmış hesablama sistemləri:
- ABAQUS —SE analizi üçün daxili postprosessorlu universal sistem;
- Analysis3D — SE analizi üçün daxili postprosessorlu universal sistem;
- ANSYS — SE analizi üçün daxili postprosessorlu universal sistem;
- COMSOL Multiphysics — SE analizi üçün daxili postprosessorlu universal sistem;
- Impact — SE analizi üçün daxili postprosessorlu universal sistem;
- MSC.Nastran — SE analizi üçün daxili postprosessorlu universal sistem;
- NEiNastran — SE analizi üçün daxili postprosessorlu universal sistem;
- NXNastran — SE analizi üçün daxili postprosessorlu universal sistem;
- NX Nastran — SE analizi üçün daxili postprosessorlu universal sistem;
- SAMCEF — SE analizi üçün daxili postprosessorlu universal siistem;
- Temper-3D — üz ölçülü konstruksiyalarda istilik sahələrinin analizi və hesablanması üçün SE sisitemi;
Üsulu icra edən proqram təminatları
[redaktə | mənbəni redaktə et]- ANSYS
- Analysis3D
- Elmer FEM solver
- Nastran
- RFEM (Ing. Software Dlubal)
- SCAD
- MatLab
- FemLab
- Femap
- LSDYNA
- QForm 2D/3D
- DSM FEM
- DSM SCROTUM
Mənbə
[redaktə | mənbəni redaktə et]Martin Mayr, Ulrich Thalhofer. Numerische Lösungsverfahren in der Praxis: FEM-BEM-FDM. Verlag:Hanser, 1993.