Düzgün beşbucaqlı

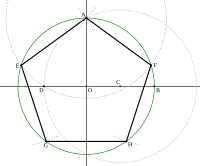
Düzgün beşbucaqlı-beş bucağı olan düzgün çoxbucaqlıdır.

Beşbucaqlının qurulması[redaktə | mənbəni redaktə et]

Xassələri[redaktə | mənbəni redaktə et]

• Xarici bucaqların ölçüləri eynidir.
• Daxili bucaqların ölçüləri eynidir.
• Tərəflərin uzunluqları eynidir.

Beşbucaqlının bir tərəfli a olarsa

Xarici və daxili bucaqları[redaktə | mənbəni redaktə et]

• Xarici bucağı

  ${\displaystyle \alpha ={\frac {360^{\circ }}{a}}\ ={\frac {360^{\circ }}{5}}\ ={72^{\circ }}}$

  • • • • • • • Daxili bucağı

                ${\displaystyle \beta ={\frac {180^{\circ }(5-2)}{a}}={\frac {180^{\circ }\cdot 3}{5}}={108^{\circ }}}$ ָָָ

Diaqonalları[redaktə | mənbəni redaktə et]

• Beşbucaqlının diaqonallarının sayı

  ${\displaystyle {\frac {5\cdot (5-3)}{2}}={5}}$

Sahəsi[redaktə | mənbəni redaktə et]

• Düzgün beşbucaqlının tərəfinin uzunluğu ${\displaystyle t}$ olarsa onun sahəsi:
• ${\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}}$

• Düzgün beşbucaqlının xaricinə kəçilmiş çevrənin radiusu R, daxilə kəçilmiş çevrənin radiusu r olarsa onun sahəsi:
• ${\displaystyle S={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}}$