Ellips

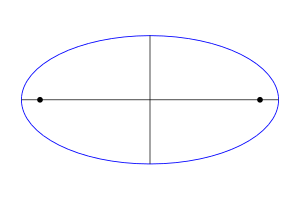
Ellips (q.yun. ἔλλειψις — endirmə, çatışmazlıq) — müstəvi üzərində fokuslar adlanan iki nöqtədən məsafələrinin cəmi sabit olub, fokuslar arasındakı məsafədən böyük qalan nöqtələrin həndəsi yeri^[1].

Düstur ilə təyini və Ellipsin kanonik tənliyi:

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.}$

Xüsusi halda ${\displaystyle a=b}$ olarsa ${\displaystyle {x^{2}}+{y^{2}}=1}$ çevrəsi alınar.

• Ellips fokusları vasitəsilə keçən və ucu ellipsə uzanan AB parçası, bu ellipsin böyük oxu adlanır. Böyük oxun uzunluğu yuxarıda göstərilən tənlikdə 2a-ya bərabərdir.
• CD parçası - perpendikulyar ellipsin böyük oxunun mərkəzindən keçən və elliə uzanan ox, ellipsin kiçik oxu adlan
• larının kəsişmə nöqtəsi oadl Abbasov eli 1706anır.
• Müstəvi üzərində ixtiyari nöqtənin fokuslardan ibarət ${\displaystyle r_{1}}$ və ${\displaystyle r_{2}}$ məsafəsi bu nöqtənin fokal radiusları adlanır.
• Məsafə tənliyi: ${\displaystyle c={\frac {|F_{1}F_{2}|}{2}}}$

Bu təyin fokus məsafəsi adlanır.

• ${\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$ təyini eliptik ölçü adlanır.
• Ellipsin diametri onun mərkəzindən keçən vətərdir. Ellipsin diametri 2 xüsusiyyətə malikdir: vətərin ortası paralel olaraq birinci diametrdən ikinci diametrə qədər uzanır. Bu halda və vətərin ortası paralel olaraq ikinci diametrdən, birinci diametrə qədər uzanır.
• İxtiyari nöqtədə ellipsin radiusu (mərkəzdən bu nöqtəyə qədər olan məsafə) aşağıdakı düstur ilə hesablanır:

${\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}$

burada ${\displaystyle \varphi }$ — bu nöqtənin radius-vektoru ilə absis oxu arasında qalan bucaqdır.

• ${\displaystyle p={\frac {b^{2}}{a}}}$ fokus parametri fokusdan keçən vətər ilə ellipsə perpendikulyar böyük oxun uzunluğunun yarısına bərabərdir.
• Kiçiyin uzunluqlar ilə və böyük yarımoxlar arasındakı əlaqə ellipsin sıxma əmsalı və ya eliptiklik adlanır:

• Optika
  • Fokuslardan birində olan mənbədən əks etdirilən işıq şüaları ikinci fokusda kəsişəcək.
  • Fokuslardan kənar olan ixtiyari mənbədən ellipsə əks etdirilən şüalar heç bir fokusda kəsişməyəcək.
• Əgər ellipsin fokusları ${\displaystyle F_{1}}$ və ${\displaystyle F_{2}}$-sə, — onda ellipsə aid olan ixtiyari X nöqtəsi ilə toxunan arasındakı bucağı, ${\displaystyle (F_{1}X)}$ düzü ilə bu toxunanın ${\displaystyle (F_{2}X)}$ düzü arasındakı bucağa bərabərdir.
• Ellipsdən keçən iki paralel düz xətt parçaları həmişə ellipsin mərkəzindən keçir. Bu da ellipsi pərgarın köməyi ilə qurmağa imkan verir. Beləki, xətlər ilə ellipsin mərkəzi, oxları, zirvələri və fokusları asan qurulur.
• Astroid, ellipsin evolyutasıdır.
• Oxları ilə ellipsin kəsişmə nöqtələri onun zirvələridir.
• Ellips eliptik əlaqəyə bərabərdir ${\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1).}$ Eliptik ellipsin uzunluğunu xarakterizə edir. Nə qədər eliptik sıfıra daha yaxın olarsa ellipsin təsvir olunması artır və əks prosesdə isə (yəni sıfırdan böyük) ellips təsviri xatırladır. Eliptik vahidə yaxın olduqda isə, bir o qədər uzadacaqlar.
• Ellipsi təsvir etmək olar:
  • çevrəyə affin dəyişikliyini tətbiq edərək;
  • çevrənin səthə ortoqonal proyeksiyası ilə;
  • Səthin və dairəvi silindrin kəsişməsi ilə;

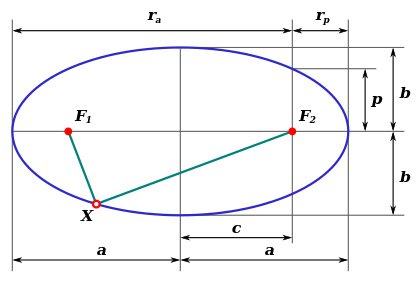
• ${\displaystyle ~{\boldsymbol {a}}}$ — böyük yarım ox;
• ${\displaystyle ~{\boldsymbol {b}}}$ — kiçik yarım ox;
• ${\displaystyle ~{\boldsymbol {c}}}$ — fokus məsafəsi (fokuslar arasındakı məsafə);
• ${\displaystyle ~{\boldsymbol {p}}}$ — fokus parametri;
• ${\displaystyle ~{\boldsymbol {r}}_{p}}$ — perifoks məsafəsi (ellipsdə fokusdan nöqtəyə qədər minimal məsafə);
• ${\displaystyle ~{\boldsymbol {r}}_{a}}$ — apofoks məsafəsi (ellipsdə fokusdan nöqtəyə qədər maksimal məsafə);

${\displaystyle ~a^{2}=b^{2}+c^{2}}$

${\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1).}$.

${\displaystyle ~p={\frac {b^{2}}{a}}}$

	${\displaystyle ~{\boldsymbol {a}}}$	${\displaystyle ~{\boldsymbol {b}}}$	${\displaystyle ~{\boldsymbol {c}}}$	${\displaystyle ~{\boldsymbol {p}}}$	${\displaystyle ~{\boldsymbol {r_{p}}}}$	${\displaystyle ~{\boldsymbol {r_{a}}}}$
${\displaystyle ~{\boldsymbol {a}}}$ – böyük yarım ox	${\displaystyle ~{\boldsymbol {a}}}$	${\displaystyle ~a={\frac {b}{\sqrt {1-e^{2}}}}}$	${\displaystyle ~a={\frac {c}{e}}}$	${\displaystyle ~a={\frac {p}{1-e^{2}}}}$	${\displaystyle ~a={\frac {r_{p}}{1-e}}}$	${\displaystyle ~a={\frac {r_{a}}{1+e}}}$
${\displaystyle ~{\boldsymbol {b}}}$ – kiçik yarım ox	${\displaystyle ~b=a{\sqrt {1-e^{2}}}}$	${\displaystyle ~{\boldsymbol {b}}}$	${\displaystyle ~b={\frac {c~{\sqrt {1-e^{2}}}}{e}}}$	${\displaystyle ~b={\frac {p}{\sqrt {1+e^{2}}}}}$	${\displaystyle ~b=r_{p}{\sqrt {\frac {1+e}{1-e}}}}$	${\displaystyle ~b=r_{a}{\sqrt {\frac {1-e}{1+e}}}}$
${\displaystyle ~{\boldsymbol {c}}}$ – fokal məsafə	${\displaystyle ~c=ae}$	${\displaystyle ~c={\frac {be}{\sqrt {1-e^{2}}}}}$	${\displaystyle ~{\boldsymbol {c}}}$	${\displaystyle ~c={\frac {pe}{1-e^{2}}}}$	${\displaystyle ~c={\frac {r_{p}e}{1-e}}}$	${\displaystyle ~c={\frac {r_{a}e}{1+e}}}$
${\displaystyle ~{\boldsymbol {p}}}$ – fokal parametr	${\displaystyle ~p=a(1-e^{2})}$	${\displaystyle ~p=b~{\sqrt {1-e^{2}}}}$	${\displaystyle ~p=c~{\frac {1-e^{2}}{e}}}$	${\displaystyle ~{\boldsymbol {p}}}$	${\displaystyle ~p=r_{p}(1+e)}$	${\displaystyle ~p=r_{a}(1-e)}$
${\displaystyle ~{\boldsymbol {r}}_{p}}$ – perifoks məsafə	${\displaystyle ~r_{p}=a(1-e)}$	${\displaystyle ~r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}}$	${\displaystyle ~r_{p}=c~{\frac {1-e}{e}}}$	${\displaystyle ~r_{p}={\frac {p}{1+e}}}$	${\displaystyle ~{\boldsymbol {r}}_{p}}$	${\displaystyle ~r_{p}=r_{a}{\frac {1-e}{1+e}}}$
${\displaystyle ~{\boldsymbol {r}}_{a}}$ – apofoks məsafə	${\displaystyle ~r_{a}=a(1+e)}$	${\displaystyle ~r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}}$	${\displaystyle ~r_{a}=c~{\frac {1+e}{e}}}$	${\displaystyle ~r_{a}={\frac {p}{1-e}}}$	${\displaystyle ~r_{a}=r_{p}~{\frac {1+e}{1-e}}}$	${\displaystyle ~{\boldsymbol {r}}_{a}}$

1. ↑ Ali riyaziyyat (lectures) (pdf). Melikov Behruz. səh. səh. 22-27. 2016-04-04 tarixində arxivləşdirilib (PDF). İstifadə tarixi: 2013-12-25. (az.)