Kristal sahə nəzəriyyəsi
Bu məqaləni vikiləşdirmək lazımdır. |
Kristal sahə nəzəriyyəsi — mahiyyətcə kimyəvi rabitənin klassik nəzəriyyəsinə yaxın olub, kompleksəmələgətirici ilə liqandlar arasında yalnız elektrostatik qarşılıqlı təsiri qəbul edir. Kristal sahə nəzəriyyəsinin riyazi hesablamaları ilk dəfə 1929-cu ildə alman alimi Bete tərəfindən aparılmışdır.
İzahı
[redaktə | mənbəni redaktə et]Klassik təsəvvürlərdən fərqli olaraq, kristal sahə nəzəriyyəsində liqandların kompleksəmələgətiricinin elektronlarına təsiri nəzərdə tutulur. başqa sözlə, kristal sahə nəzəriyyəsi kompleksəmələgəlmə prosesi ilə əlaqədar olaraq bütün hadisələri kompleksəmələgətiricinin sərbəst ionlarının (məsələn, Co3+, Fe2+ və s.) liqandların elektrostatik sahəsinə düşməsi zamanı elektron təbəqələrində gedən dəyişikliklə izah etməyə çalışır. Müəyyən edilmişdir ki, kompleks birləşmələrdə liqandların elektrostatik sahəsi, bərk maddələrin kristal şəbəkələrini təşkil edən ionların yerləşdiyi elektrostatik sahə ilə tamamilə oxşardır. Məsələn, [Fe(CN)6]4--də Fe2+ ionu altı liqandın elektrostatik sahəsi təsirində olduğu kimi, NaCl-in kristal şəbəkəsində Na+ ionu da altı Cl- ionun elektrostatik sahəsində yerləşir. Həm də hər iki halda fəza mərkəzində müsbət yüklü ion yerləşən oktaedr əmələ gəlir. Beləliklə, kompleks birləşmələrdə kompleksəmələgətirici ionun vəziyyəti ilə kristal şəbəkələrində müsbət ionların vəziyyəti arasında belə oxşarlığın mövcudluğuna əsasən kompleks birləşmələrin tədqiqi ilə məşğul olan bu nəzəriyyə kristal sahə nəzəriyyəsi adını almışdır.
Liqandların yaratdığı sahə qüvvətli olduqda Δ qiyməti də böyük olur. Liqandların sahəsi ilə Δ qiymətinin arasındakı emprik asılılıq aşağıdakı kimidir:
I− < Br− < S2− < SCN− < Cl− < NO3− < N3− < F− < OH− < C2O42− < H2O < NCS− < CH3CN < py < NH3 < en < bipy < phen < NO2− < PPh3 < CN− < CO
Δ qiyməti artır.
Kristal sahədə d-orbitallarının parçalanması
[redaktə | mənbəni redaktə et]Kristal sahə nəzəriyyəsinə müvafiq olaraq, d-elementlərinkompleksəmələgətirici ionu liqandların elektrostatik sahəsinə (kristal sahəyə) düşdükdə, onun d-orbitallarında parçalanma baş verir.
| oktaedrik | pentaqonal bipiramidal | kvadrat |
|---|---|---|
 |
 |
 |
 |
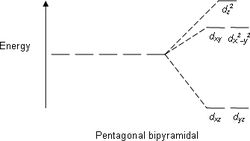 |
 |
| kvadrat | kvadrat-piramidal | tetraedrik |
 |
 |
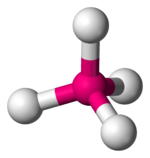 |
 |
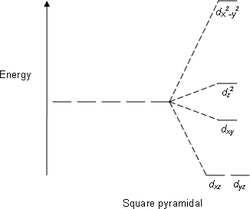 |
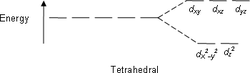 |
 | ||
 |
Mənbə
[redaktə | mənbəni redaktə et]- Z. Qarayev "Qeyri-üzvi kimya", Maarif-1975