Tərs triqonometrik funksiyalar (dairəvi funksiya , arkfunksiya ) — triqonometrik funksiyalar tərsinə çevrilə bilən riyazi funksiyalardır . Tərs triqonometrik funksiyalara əsasən altı funksiya daxildir:
arksinus (
a
r
c
s
i
n
x
{\displaystyle \mathrm {arcsin} \,x}
x
{\displaystyle x}
arkkosinus (
a
r
c
c
o
s
x
{\displaystyle \mathrm {arccos} \,x}
x
{\displaystyle x}
arktangens (
a
r
c
t
a
n
x
{\displaystyle \mathrm {arctan} \,x}
a
r
c
t
g
x
{\displaystyle \mathrm {arctg} \,x}
arkkotangens (
a
r
c
c
o
t
x
{\displaystyle \mathrm {arccot} \,x}
a
r
c
c
o
t
a
n
x
{\displaystyle \mathrm {arccotan} \,x}
a
r
c
c
t
g
x
{\displaystyle \mathrm {arcctg} \,x}
arksekans (
a
r
c
s
e
c
x
{\displaystyle \mathrm {arcsec} \,x}
arkkosekans (
a
r
c
c
s
c
x
{\displaystyle \mathrm {arccsc} \,x}
a
r
c
c
o
s
e
c
x
{\displaystyle \mathrm {arccosec} \,x}
Triqonometrik funksiyaların adının qarışındakı "arc" sözü ( lat. arc usalm. Karl Scherffer ; 1716—1783) daxil etmişdir.
arcsin
x
+
arccos
x
=
π
2
{\displaystyle \arcsin x+\arccos x={\frac {\pi }{2}}}
arctan
x
+
arccot
x
=
π
2
{\displaystyle \operatorname {arctan} \,x+\operatorname {arccot} \,x={\frac {\pi }{2}}}
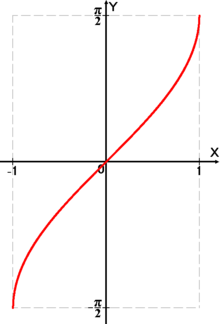
y
=
arcsin
x
{\displaystyle y=\arcsin x}
Arksinus - m ədədinin x bucağının qiymətinə , radian ifadəsinə deyilir, hansı ki,
sin
x
=
m
,
−
π
2
⩽
x
⩽
π
2
,
|
m
|
⩽
1.
{\displaystyle \sin x=m,\,-{\frac {\pi }{2}}\leqslant x\leqslant {\frac {\pi }{2}},\,|m|\leqslant 1.}
y
=
sin
x
{\displaystyle y=\sin x}
y
=
arcsin
x
{\displaystyle y=\arcsin x}
sin
(
arcsin
x
)
=
x
{\displaystyle \sin(\arcsin x)=x\qquad }
−
1
⩽
x
⩽
1
,
{\displaystyle -1\leqslant x\leqslant 1,}
arcsin
(
sin
y
)
=
y
{\displaystyle \arcsin(\sin y)=y\qquad }
−
π
2
⩽
y
⩽
π
2
,
{\displaystyle -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},}
D
(
arcsin
x
)
=
[
−
1
;
1
]
{\displaystyle D(\arcsin x)=[-1;1]\qquad }
E
(
arcsin
x
)
=
[
−
π
2
;
π
2
]
{\displaystyle E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad }
arcsin
(
−
x
)
=
−
arcsin
x
{\displaystyle \arcsin(-x)=-\arcsin x\qquad }
0
<
x
⩽
1
{\displaystyle 0<x\leqslant 1}
arcsin
x
>
0
{\displaystyle \arcsin x>0}
x
=
0
{\displaystyle x=0}
arcsin
x
=
0
{\displaystyle \arcsin x=0}
−
1
⩽
x
<
0
{\displaystyle -1\leqslant x<0}
arcsin
x
<
0
{\displaystyle \arcsin x<0}
arcsin
x
=
{
arccos
1
−
x
2
,
0
⩽
x
⩽
1
−
arccos
1
−
x
2
,
−
1
⩽
x
<
0
{\displaystyle \arcsin x=\left\{{\begin{matrix}\arccos {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\-\arccos {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.}
arcsin
x
=
arctg
x
1
−
x
2
{\displaystyle \arcsin x=\operatorname {arctg} {\frac {x}{\sqrt {1-x^{2}}}}}
arcsin
x
=
{
arcctg
1
−
x
2
x
,
0
<
x
⩽
1
arcctg
1
−
x
2
x
−
π
,
−
1
⩽
x
<
0
{\displaystyle \arcsin x=\left\{{\begin{matrix}\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}}-\pi ,\qquad -1\leqslant x<0\end{matrix}}\right.}
y
=
sin
x
{\displaystyle y=\sin x}
y
=
arcsin
x
{\displaystyle y=\arcsin x}
[
−
π
2
;
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}
y
=
sin
x
{\displaystyle y=\sin x}
[
−
π
2
;
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}
y
=
arcsin
x
{\displaystyle y=\arcsin x}
[
−
π
2
;
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}
y
=
sin
x
{\displaystyle y=\sin x}
y
=
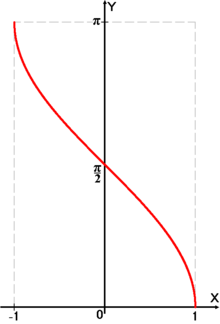
arccos
x
{\displaystyle y=\arccos x}
Arkkosinus - Elə m ədədinə deyilir ki, radian ölçüsündə x bucağına bərabərdir, hansı ki,
cos
x
=
m
,
0
⩽
x
⩽
π
,
|
m
|
⩽
1
{\displaystyle \cos x=m,\qquad 0\leqslant x\leqslant \pi ,|m|\leqslant 1}
y
=
cos
x
{\displaystyle y=\cos x}
y
=
arccos
x
{\displaystyle y=\arccos x}
cos
(
arccos
x
)
=
x
{\displaystyle \cos(\arccos x)=x}
−
1
⩽
x
⩽
1
{\displaystyle -1\leqslant x\leqslant 1}
arccos
(
cos
y
)
=
y
{\displaystyle \arccos(\cos y)=y}
0
⩽
y
⩽
π
{\displaystyle 0\leqslant y\leqslant \pi }
D
(
arccos
x
)
=
[
−
1
;
1
]
,
{\displaystyle D(\arccos x)=[-1;1],}
E
(
arccos
x
)
=
[
0
;
π
]
.
{\displaystyle E(\arccos x)=[0;\pi ].}
arccos
(
−
x
)
=
π
−
arccos
x
{\displaystyle \arccos(-x)=\pi -\arccos x}
(
0
;
π
2
)
{\displaystyle \left(0;{\frac {\pi }{2}}\right)}
arccos
x
>
0
{\displaystyle \arccos x>0}
−
1
⩽
x
<
1
{\displaystyle -1\leqslant x<1}
arccos
x
=
0
{\displaystyle \arccos x=0}
x
=
1
{\displaystyle x=1}
arccos
x
=
π
2
−
arcsin
x
.
{\displaystyle \arccos x={\frac {\pi }{2}}-\arcsin x.}
arccos
x
=
{
arcsin
1
−
x
2
,
0
⩽
x
⩽
1
π
−
arcsin
1
−
x
2
,
−
1
⩽
x
<
0
{\displaystyle \arccos x=\left\{{\begin{matrix}\arcsin {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\\pi -\arcsin {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.}
arccos
x
=
{
arctg
1
−
x
2
x
,
0
<
x
⩽
1
π
+
arctg
1
−
x
2
x
,
−
1
⩽
x
<
0
{\displaystyle \arccos x=\left\{{\begin{matrix}\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\pi +\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad -1\leqslant x<0\end{matrix}}\right.}
arccos
x
=
2
arcsin
1
−
x
2
{\displaystyle \arccos x=2\arcsin {\sqrt {\frac {1-x}{2}}}}
arccos
x
=
2
arccos
1
+
x
2
{\displaystyle \arccos x=2\arccos {\sqrt {\frac {1+x}{2}}}}
arccos
x
=
2
arctg
1
−
x
1
+
x
{\displaystyle \arccos x=2\operatorname {arctg} {\sqrt {\frac {1-x}{1+x}}}}
y
=
arctan
x
{\displaystyle y=\operatorname {arctan} \,x}
y
=
arctan
x
{\displaystyle y=\operatorname {arctan} x}
y
=
arctan
x
{\displaystyle y=\operatorname {arctan} x}
tan
(
arctan
x
)
=
x
{\displaystyle \operatorname {tan} \,(\operatorname {arctan} \,x)=x}
x
∈
R
{\displaystyle x\in \mathbb {R} }
arctan
(
tan
y
)
=
y
{\displaystyle \operatorname {arctan} \,(\operatorname {tan} \,y)=y}
−
π
2
<
y
<
π
2
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}
D
(
arctan
x
)
=
(
−
∞
;
∞
)
,
{\displaystyle D(\operatorname {arctan} \,x)=(-\infty ;\infty ),}
E
(
arctan
x
)
=
(
−
π
2
;
π
2
)
{\displaystyle E(\operatorname {arctan} \,x)=\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)}
arctan
(
−
x
)
=
−
arctan
x
{\displaystyle \operatorname {arctan} (-x)=-\operatorname {arctan} x\qquad }
arctan
x
=
arcsin
x
1
+
x
2
{\displaystyle \operatorname {arctan} x=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}}
arctan
x
=
arccos
1
1
+
x
2
{\displaystyle \operatorname {arctan} x=\arccos {\frac {1}{\sqrt {1+x^{2}}}}}
arctan
x
=
arccot
1
x
{\displaystyle \operatorname {arctan} x=\operatorname {arccot} {\frac {1}{x}}}
arctan
x
=
−
i
arcth
i
x
{\displaystyle \operatorname {arctan} x=-i\operatorname {arcth} {ix}}
arcth
{\displaystyle \operatorname {arcth} }
arcth
x
=
i
arctan
i
x
{\displaystyle \operatorname {arcth} x=i\operatorname {arctan} {ix}}
...
y
=
arccot
x
.
{\displaystyle y=\operatorname {arccot} x.}
y
=
arccot
x
{\displaystyle y=\operatorname {arccot} \,x}
y
=
arccot
x
{\displaystyle y=\operatorname {arccot} \,x}
cot
(
arccot
x
)
=
x
{\displaystyle \operatorname {cot} \,(\operatorname {arccot} \,x)=x}
x
∈
R
{\displaystyle x\in \mathbb {R} }
arccot
(
cot
y
)
=
y
{\displaystyle \operatorname {arccot} \,(\operatorname {cot} \,y)=y}
0
<
y
<
π
{\displaystyle 0<y<\pi }
D
(
arccot
x
)
=
(
−
∞
;
∞
)
,
{\displaystyle D(\operatorname {arccot} \,x)=(-\infty ;\infty ),}
E
(
arccot
x
)
=
(
0
;
π
)
.
{\displaystyle E(\operatorname {arccot} \,x)=(0;\pi ).}
arccot
(
−
x
)
=
π
−
arccot
x
{\displaystyle \operatorname {arccot} \,(-x)=\pi -\operatorname {arccot} \,x}
(
0
;
π
2
)
.
{\displaystyle \left(0;{\frac {\pi }{2}}\right).}
arccot
x
>
0
{\displaystyle \operatorname {arccot} \,x>0}
x
{\displaystyle x}
arccot
x
=
{
arcsin
1
1
+
x
2
,
x
⩾
0
π
−
arcsin
1
1
+
x
2
,
x
<
0
{\displaystyle \operatorname {arccot} \,x=\left\{{\begin{matrix}\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\geqslant 0\\\pi -\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x<0\end{matrix}}\right.}
arccot
x
=
π
/
2
−
arccot
x
.
{\displaystyle \operatorname {arccot} x=\pi /2-\operatorname {arccot} x.}
...
arcsec
(
x
)
=
arccos
(
1
x
)
{\displaystyle \mathop {\operatorname {arcsec} } \,(x)\,=\operatorname {arccos} \left({\frac {1}{x}}\right)}
arccsc
(
y
)
=
arcsin
(
1
y
)
{\displaystyle \mathop {\operatorname {arccsc} } \,(y)\,=\operatorname {arcsin} \left({\frac {1}{y}}\right)}
(
arcsin
x
)
′
=
1
1
−
x
2
.
{\displaystyle (\arcsin x)'={\frac {1}{\sqrt {1-x^{2}}}}.}
(
arccos
x
)
′
=
−
1
1
−
x
2
.
{\displaystyle (\arccos x)'=-{\frac {1}{\sqrt {1-x^{2}}}}.}
(
arctan
x
)
′
=
1
1
+
x
2
.
{\displaystyle (\operatorname {arctan} \,x)'={\frac {1}{\ 1+x^{2}}}.}
(
arccot
x
)
′
=
−
1
1
+
x
2
.
{\displaystyle (\operatorname {arccot} \,x)'=-{\frac {1}{\ 1+x^{2}}}.}
x həqiqi və kompleks qiymətlər üçün :
∫
arcsin
x
d
x
=
x
arcsin
x
+
1
−
x
2
+
C
,
∫
arccos
x
d
x
=
x
arccos
x
−
1
−
x
2
+
C
,
∫
arctan
x
d
x
=
x
arctan
x
−
1
2
ln
(
1
+
x
2
)
+
C
,
∫
arccot
x
d
x
=
x
arccot
x
+
1
2
ln
(
1
+
x
2
)
+
C
,
∫
arcsec
x
d
x
=
x
arcsec
x
−
ln
(
x
(
1
+
x
2
−
1
x
2
)
)
+
C
,
∫
arccsc
x
d
x
=
x
arccsc
x
+
ln
(
x
(
1
+
x
2
−
1
x
2
)
)
+
C
.
{\displaystyle {\begin{aligned}\int \arcsin x\,dx&{}=x\,\arcsin x+{\sqrt {1-x^{2}}}+C,\\\int \arccos x\,dx&{}=x\,\arccos x-{\sqrt {1-x^{2}}}+C,\\\int \operatorname {arctan} \,x\,dx&{}=x\,\operatorname {arctan} \,x-{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arccot} \,x\,dx&{}=x\,\operatorname {arccot} \,x+{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\,\right)\!\right)+C,\\\int \operatorname {arccsc} \,x\,dx&{}=x\,\operatorname {arccsc} \,x+\ln \left(x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\,\right)\!\right)+C.\end{aligned}}}
x ≥ 1 həqiqi qiymətlər üçün:
∫
arcsec
x
d
x
=
x
arcsec
x
−
ln
(
x
+
x
2
−
1
)
+
C
,
∫
arccsc
x
d
x
=
x
arccsc
x
+
ln
(
x
+
x
2
−
1
)
+
C
.
{\displaystyle {\begin{aligned}\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C,\\\int \operatorname {arccsc} \,x\,dx&{}=x\,\operatorname {arccsc} \,x+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C.\end{aligned}}}
Əgər üçbucağın tərəfləri verilərsə, onda üçbucağın bucaqlarının tapılması üçün tərs triqonometrik funksiyalarından istifadə edilir. Məsələn: Kosinuslar teoremi ilə tapılır.
Düzbucaqlı üçbucaqda, bucağı tərəflər arasındakı münasibət vasitəsilə bu funksiyalarla alınır:
α = arcsin (a/c) = arccos (b/c) = arctan (a/b) = arccsc (c/a) = arcsec (c/b) = arccot (b/a) Kompleks arqumentli tərs triqonometrik funksiyaların dəyişəninin həlli üçün natural loqarifmlərlə verilməsi düsturları:
arcsin
z
=
−
i
ln
(
i
z
+
1
−
z
2
)
=
π
2
−
i
ln
(
z
+
z
2
−
1
)
,
{\displaystyle {\begin{aligned}\arcsin z&{}=-i\ln(iz+{\sqrt {1-z^{2}}})={\frac {\pi }{2}}-i\ln(z+{\sqrt {z^{2}-1}}),\end{aligned}}}
arccos
z
=
π
2
+
i
ln
(
i
z
+
1
−
z
2
)
,
{\displaystyle {\begin{aligned}\arccos z&{}={\dfrac {\pi }{2}}+i\ln(iz+{\sqrt {1-z^{2}}}),\end{aligned}}}
arctan
z
=
i
2
(
ln
(
1
−
i
z
)
−
ln
(
1
+
i
z
)
)
,
{\displaystyle {\begin{aligned}\operatorname {arctan} \,z&{}={\dfrac {i}{2}}(\ln(1-iz)-\ln(1+iz)),\end{aligned}}}
arccot
z
=
i
2
(
ln
(
z
−
i
z
)
−
ln
(
z
+
i
z
)
)
,
{\displaystyle {\begin{aligned}\operatorname {arccot} \,z&{}={\dfrac {i}{2}}\left(\ln \left({\dfrac {z-i}{z}}\right)-\ln \left({\dfrac {z+i}{z}}\right)\right),\end{aligned}}}
arcsec
z
=
arccos
(
z
−
1
)
=
π
2
+
i
ln
(
1
−
1
z
2
+
i
z
)
,
{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left(z^{-1}\right)={\dfrac {\pi }{2}}+i\ln \left({\sqrt {1-{\dfrac {1}{z^{2}}}}}+{\dfrac {i}{z}}\right),\end{aligned}}}
arccsc
z
=
arcsin
(
z
−
1
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
.
{\displaystyle {\begin{aligned}\operatorname {arccsc} \,z&{}=\arcsin \left(z^{-1}\right)=-i\ln \left({\sqrt {1-{\dfrac {1}{z^{2}}}}}+{\dfrac {i}{z}}\right).\end{aligned}}}






















![{\displaystyle D(\arcsin x)=[-1;1]\qquad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd3f4bf3e28749594b902927c25d875de43acb55)
![{\displaystyle E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35cf0029d59f77e2edbf4e49629cd8563aa42d0b)










![{\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8953e7a70dae484772b5a2b5cab77216226235d)







![{\displaystyle D(\arccos x)=[-1;1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91792aac1d518a870d412d3e7d0e9fb7f53e5887)
![{\displaystyle E(\arccos x)=[0;\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc41ed783f7a7698b111ce8f052693448a23a75c)




















































