Süni neyron

Süni neyron — bioloji neyronun modeli kimi irəli sürülən riyazi funksiyadır. Süni neyronlar süni neyron şəbəkədə təsisedici bölmədir. Onlar istifadə olunmuş xarakterik modeldən asılı olaraq yarımxətti hissəli, Nv neyron, ikilik neyron, xətti hüdud funksiyası və Makkallok-Pitts neyronu kimi adlandırıla bilər. Süni neyron bir və ya daha çox girişdən (dendriti təsvir edir) qəbul edir və çıxışı (neyronun aksonunu təsvir edir) hasil etmək üçün onları cəmləyir. Adətən hər bir qovşağın cəmi onların çəkisi olur və cəm aktivləşdirmə funksiyası və ya ötürmə funksiyası kimi məlum olan qeyri-xətti funksiya kimi verilir. Ötürmə funksiyası adətən siqmoid formasında olur , ancaq onlar həmçinin hissə-hissə müəyyən olunmuş xətti funksiyalar , keçid funksiyaları və ya digər xətti funksiyalar formasında verilə bilər. Onlar həmiçinin monoton artan, fasiləsiz, differensial və məhdud funksiyalarla verilə bilər.

Süni neyronların ötürmə funksiyaları xətti sistemlərin ötürmə funksiyaları ilə qarışdırılmamalıdır.

Süni neyronların riyazi modeli ilk dəfə 1943-cü ildə Uorren Makkallok^[ing.] və Volter Pitts^[ing.] tərəfindən təklif edilib. Bu model xüsusi olaraq, beyində "sinir şəbəkələrinin" hesablama modeli kimi düşünülmüşdü.^[1] Müəlliflər göstərdilər ki, belə elementli şəbəkələr say və məntiqi əməliyyatları yerinə yetirə bilər.^[2].

Süni neyron şəbəkərlə yenilik və mühüm bir cəhət Frenk Rozenblat tərəfindən inkişaf etdirilmiş perseptron idi. Bu model artıq neyronlarda daha çevik çəki dəyərləri sayılırdı və adaptiv potensial imkanlı maşınlarda istifadə olunurdu.

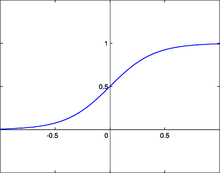
İstifadə olunan şəbəkənin topologiyasından asılı olaraq, müxtəlif növlü fəallaşma funksiyalarından istifadə oluna bilər. Belə bir funksiya kimi hissə-hissə xətti funksiya, siqmoid funksiyası (yarımxətti funksiya), vahid sıçrayış funksiyası ola bilər. Ümumiyyətlə fəallaşma funksiyaları monoton olaraq, artır.

Neyronun çıxışındakı siqnal onun girişindəki siqnalların cəmi ilə bağlıdır.

${\displaystyle f(x)=tx}$,

burada ${\displaystyle t}$ — funksiyanın parametridir. Bu funksiyanı düsturla aşağıdakı kimi ifadə etmək olar^[3]:

${\displaystyle f(x)={\begin{cases}0&{\text{if }}x\leq 0\\1&{\text{if }}x\geq 1\\x&{\text{else}}\end{cases}}}$

Bu halda hər iki ox üzrə funksiyanın sürüşdürülməsi mümkündür.

Vahid sıçrayış funksiyasından istifadə edən neyronlar girişlərin əmsallara vurulmuş cəmi hüdud kəmiyyətinə çatanda ani olaraq vəziyyətlərini "0"-dan "1"-ə dəyişirlər. Laylı süni neyron şəbəkələrin ən birinci nümayəndəsi yalnız bu cür neyronlardan ibarət olan perseptrondur. Bu funksiyanın riyazi yazılışı aşağıdakı kimidir:

${\displaystyle f(x)={\begin{cases}1&{\text{if }}x\geq T\\0&{\text{else}}\end{cases}}}$

Bu funksiya fəallaşma funksiyasının verilməsinin ən çox yayılmış formasıdır. Ümumi giriş -∞ yaxınlaşdıqda fəallaşma səviyyəsi sıfıra yaxınlaşır, ümumi girişin çox böyük qiymətlərində fəallaşma səviyyəsi praktiki olaraq, "1"-ə bərabərdir. Riyazi ifadəsi aşağıdakı kimidir:

${\displaystyle \sigma (x)={\frac {1}{(1+\exp(-tx))}}}$

Məhdud ötürmə funksiyalı neyron müxtəlif məntiq funksiyaları ilə modelləşdirilə bilər. Giriş siqnallarının çəkilərini və həssaslığın məhdudluğunu verib, neyronun giriş siqnallarının üstündə konyuksiyanı (məntiqi "və") və dizyunksiyanı (məntiqi "və ya"), eləcə də məntiqi inkarı^[4] yerinə yetirmək olar. Arqumentlərin istənilən sayında istənilən məntiq funksiyasının modelini hazırlamaq üçün bu üç əməliyyat kifayətdir.

• Süni neyron şəbəkələr