
















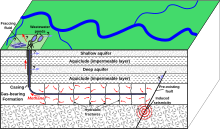

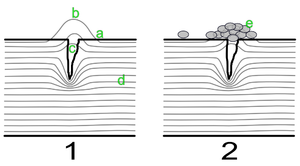







lay enerjisinin təsiri ilə quyulardan neftin, qaz-kondensatın yer səthinə qaldırılması.
Полностью »...suların mövcudluğu, məhsuldar laydakı kövrək süxur və s. bu üsulun çatışmayan cəhətləridir.
Полностью »



























i. fountain; su ~ı a fountain of water; neft ~ı oil-gusher; ~ vurmaq to gush, to spring* forth
Полностью »is. və sif. Neft istehsalı ilə, neft çıxarılması ilə məşğul olan. Neftçıxarma briqadası. // Neft istehsalı ilə, neft çıxarılması ilə əlaqədar olan. Ne
Полностью »I прил. нефтедобывающий. Neftçıxarma sənayesi нефтедобывающая промышленность II сущ. нефтедобыча. Neftçıxarma planı план нефтедобычи
Полностью »neftin və onunla birgə çıxan qazların Yer təkindən çıxarılması (hasilatı), toplanması və qabaqcadan emala hazırlanması (yəni sudan və bərk qatışıqlard
Полностью »...üçün ən geniş yayılmış üsul. Bu üsula dərinliyi 3500 m-ə qədər olan quyulardan neft çıxarılır. Dərinlik nasosu adi birtəsirli porşenli nasosdur. Dəri
Полностью »...səthinə qaldırılması üsulu. T.n.-dan əsasən, kiçik təzyiqli və yüksək özlülüklü nefti olan layların işlənməsində istifadə olunur. Bax: Təkrar istisma
Полностью »fontan vuran neft və qaz quyularının ağzını kipləşdirmək, onlara nəzarət etmək və istismar rejimini tənzimləmək məqsədi ilə istifadə olunan quyuüstü a
Полностью »...çıxaranda neftli laylardan ayrılan qazın genişlənməsi nəticəsində fontan vuran quyu.
Полностью »təbii obyektlərdə /əsasən kömür, ağac, sümük qalıqlarında və s./ C14 izotopunun nisbi miqdarının öyrənilməsinə əsaslanan, etmə üsul
Полностью »tərcümə haqqında elmin əsas kateqoriyalarından biri. Tərcümə üsulu obyektin mövcud olan tərcümə fəaliyyə- tində bir dildən digərinə keçidin qanuna
Полностью »cari aktivin dəyərləndirilməsində müqayisə oluna bilən aktivlərin istifadə edilməsi üsulu.
Полностью »Comparables method Cari aktivin dəyərləndiril məsində (o cümlədən ilkin yerləşdirilən qiymətli kağızların qiymətinin müəyyənləşdirilməsində) təzəlikdə
Полностью »bir qrup mütəxəssis tərəfindən aparılan zehni hücum prosesində qərarların generasiyasına və ekspert qiymətləndirmələrindən çıxış edərək, ən yaxşı qəra
Полностью »(ixtisarı …la, …lə) qoş. Qoşulduğu sözlə bəzən (samitlə qurtaranda) bitişik, bəzən də (saitlə qurtaranda) ayrı yazılıb aşağıdakı mənalarda işlənir: a)
Полностью »послел. (слитное написание -la, -lə): 1. с (со), вместе с (указывает на совместность). Kimlə yanaşı getmək идти рядом с кем, Eyvazla Gülşən Эйваз с Гю
Полностью »(ixtisarı ...la, ...lə) къушм. 1. -ал(ди), -уналди, -далди, -унив, -ув(ди), -ив(ди), -униз, -див; -дихъ; barmağı ilə göstərmək тупӀув(ди) къалурун; əl
Полностью »(-la, -lə) qoş. avec ; maraqla avec intérêt, de ; par ; en ; avtobusla getmək aller vi (ê) en autobus
Полностью »Cığataylarda ilə sözü rus dilindəki “связанный” kəlməsinə uyğun mənada işlədilib. Yəqin ki, bu söz ilmək (ilişdirmək, bağlamaq) sözünün kökündəki il
Полностью »fiqhdə hər hansı bir kişinin öz arvadına müəyyən müddətdə yaxınlaşmayacağı barəsində verdiyi sözdür. Bu müddət dörd ay olur
Полностью »Laboratoriya müayinələrinin aparılması vasitəsilə toxumun sortluq təmizliyinin və onun müəyyən sorta mənsub olmasının təyin edilməsi
Полностью »with all one’s being / with all one’s heart and soul / with all one’s body ad soul / from the bottom of one’s heart / with bag and baggage / with all
Полностью »əsas vəsaitlərin istismarının başlanğıcında hesablanan amortizasiya, istismar müddətinin sonunda hesablanan amortizasiyadan daha çox olmasına əsaslana
Полностью »digər, xarici dildə uyğunluğu nəzərdə tutan çıxarışda denotatın identifikasiyası, obyektiv olaraq bir dildən o biri dilə qanunauyğun şəkildə mövcud ke
Полностью »...фонтан. Брызги фонтана. 2) Архитектурное сооружение, обрамляющее бьющую струю воды; устройство для подачи воды и её налива. Сквер украшен фонтаном. П
Полностью »...турбадай винелди акъатиз гадар жезвай цин ва я маса жими затIунин гул, хел, мес. нафтIадин фонтан. 2. пер. акьалтI тийиз, булвилелди акъатзавай с
Полностью »amortizasiyanın hesablanması üsulu olub, əsas vəsaitlərin ehtimal olunan istifadə müddətinin azalma istiqamətində hesablanması və həmin illərin hesabl
Полностью »obyektin amortizasiya xərclərinin onun istifadə xidməti müddəti üzrə bərabər silinməsidir.
Полностью »1948 ildə K. K. Markov tərəfindən təklif edilmişdir. Mövcud relyef elementlərini müşahidə etdiyimiz səviyyə ilə onun ilkin yarandığı səviyyə arasındak
Полностью »см. фонтан; в функц. сказ. разг. О ком-, чём-л. не очень хорошем, среднем по качеству. Домик не ф. Твой приятель не ф.
Полностью »is. Neftçıxarma sənayesi işçisi. Neftçıxaranlar bu gün təmirçilərin işindən çox razı qalmışdılar. (Qəzetlərdən).
Полностью »прил. neftçıxarma -i[-ı]; нефтедобывающая промышленность neftçıxarma sənayesi.
Полностью »...ehmallı, üsulla, ehtiyatla işgörən, hərəkət edən. Üsullu adam. Üsullu hərəkət. 2. bax üsulluca. [Hacı Murad:] Ay ayı oğlu ayı, üsullu tərpənə bilmirs
Полностью »разг. I прил. осторожный. Üsullu adam осторожный человек, üsullu hərəkət осторожные действия II нареч. осторожно. Üsullu tərpənmək действовать осторож
Полностью »I. s. methodical, orderly II. z. 1. methodically, 2. carefully, cautiously, guardedly
Полностью »...ütülənmiş. Daxiliyyə naziri ütülü ağ dəsmalını çıxarıb boyunboğazından sel kimi axan təri sildi. S.Rəhimov.
Полностью »ə. 1) hüquqşünas; 2) islam dini təriqətçilərindən biri; 3) bu təriqətə mənsub olan müsəlman.
Полностью »...küsülüyəm. M.F.Axundzadə. Leyk gəl indi biz əyri oturaq, düz danışaq; Elə bil küsülü idik, gəl təzədən bir barışaq. S.Ə.Şirvani. □ Küsülü kimi – sank
Полностью »прил. обиженный, поссорившийся, в ссоре; küsülü olmaq kimlə быть в ссоре с кем, onlar küsülüdülər они в ссоре, mən onunla küsülüyəm я в ссоре с ним
Полностью »...grudge; ~ salmaq to bear* a grudge, to have* a grudge (against), to be* at variance (with); to be* at odds (with)
Полностью »KÜSÜLÜ – BARIŞIQLI Küsülü qardaş, gəl yükü çataq, yenə küsümüz küsü (Ata. sözü); Barışıqlı məsələsinin üstündən keçdilər (“Azərbaycan”).
Полностью »məktəb proqramı kursunu ekstern yolu ilə (üsulu ilə) keçərək imtahan vermə üsulu.
Полностью »...stansiyası компрессорная станция, kompressor üsulu ilə neftçıxarma компрессорная добыча нефти, kompressor yağı компрессорное масло
Полностью »...müşahidə edilmiş / olunmuş, müşahidə yolu / üsulu ilə əldə edilmiş; ~ result müşahidə yolu / üsulu ilə əldə edilmiş nəticə
Полностью »müəssisənin gəlirindən xərclərini çıxmaq üsulu ilə hesablanır.
Полностью »...процесс bessemerləmə prosesi; 2. bessemerləmə üsulu ilə alınan; бессемеровая сталь bessemerləmə üsulu ilə alınan polad.
Полностью »