Tərs triqonometrik funksiyalar
Tərs triqonometrik funksiyalar (dairəvi funksiya, arkfunksiya) — triqonometrik funksiyalar tərsinə çevrilə bilən riyazi funksiyalardır. Tərs triqonometrik funksiyalara əsasən altı funksiya daxildir:
arksinus (
a
r
c
s
i
n
x
{\displaystyle \mathrm {arcsin} \,x}
— bu bucağın sinusu
x
{\displaystyle x}
-ə bərabərdir)
arkkosinus (
a
r
c
c
o
s
x
{\displaystyle \mathrm {arccos} \,x}
— bu bucağın kosinusu
x
{\displaystyle x}
-ə bərabərdir)
arktangens (
a
r
c
t
a
n
x
{\displaystyle \mathrm {arctan} \,x}
, bəzi ədəbiyyatlarda
a
r
c
t
g
x
{\displaystyle \mathrm {arctg} \,x}
)
arkkotangens (
a
r
c
c
o
t
x
{\displaystyle \mathrm {arccot} \,x}
və ya
a
r
c
c
o
t
a
n
x
{\displaystyle \mathrm {arccotan} \,x}
, bəzi ədəbiyyatlarda
a
r
c
c
t
g
x
{\displaystyle \mathrm {arcctg} \,x}
)
arksekans (
a
r
c
s
e
c
x
{\displaystyle \mathrm {arcsec} \,x}
)
arkkosekans (
a
r
c
c
s
c
x
{\displaystyle \mathrm {arccsc} \,x}
, bəzi ədəbiyyatlarda
a
r
c
c
o
s
e
c
x
{\displaystyle \mathrm {arccosec} \,x}
)
Triqonometrik funksiyaların adının qarışındakı "arc" sözü ( lat. arcus — ox, qövs, qövsəoxşar xətt) bu funksiyaları tərs triqonometrik funksiyaların adına çevirir. Bu onunla bağlıdır ki, tərs triqonometrik funksiyaların həndəsi qiyməti vahid çevrənin qövsünün uzunluğu ilə əlaqələndirmək olar. Tərs triqonometrik funksiyalar anlayışını Laqranj köməyi ilə Avstriya riyaziyyatçısı Karla Şerfer (alm. Karl Scherffer; 1716—1783) daxil etmişdir.
arcsin
x
+
arccos
x
=
π
2
{\displaystyle \arcsin x+\arccos x={\frac {\pi }{2}}}
arctan
x
+
arccot
x
=
π
2
{\displaystyle \operatorname {arctan} \,x+\operatorname {arccot} \,x={\frac {\pi }{2}}}
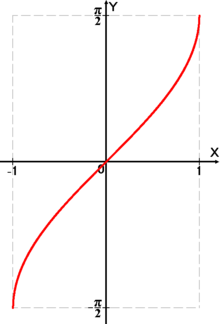
Arksinus - m ədədinin x bucağının qiymətinə , radian ifadəsinə deyilir, hansı ki,
sin
x
=
m
,
−
π
2
⩽
x
⩽
π
2
,
|
m
|
⩽
1.
{\displaystyle \sin x=m,\,-{\frac {\pi }{2}}\leqslant x\leqslant {\frac {\pi }{2}},\,|m|\leqslant 1.}
y
=
sin
x
{\displaystyle y=\sin x}
funksiyası bütün ədəd oxunda kəsilməz və məhduddur.
y
=
arcsin
x
{\displaystyle y=\arcsin x}
funksiyası ciddi artandır.
sin
(
arcsin
x
)
=
x
{\displaystyle \sin(\arcsin x)=x\qquad }
−
1
⩽
x
⩽
1
,
{\displaystyle -1\leqslant x\leqslant 1,}
arcsin
(
sin
y
)
=
y
{\displaystyle \arcsin(\sin y)=y\qquad }
−
π
2
⩽
y
⩽
π
2
,
{\displaystyle -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},}
D
(
arcsin
x
)
=
[
−
1
;
1
]
{\displaystyle D(\arcsin x)=[-1;1]\qquad }
(təyin oblastı),
E
(
arcsin
x
)
=
[
−
π
2
;
π
2
]
{\displaystyle E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad }
(qiymətlər çoxluğu).