Hiperbolik funksiyalar
Hiperbolik funksiyalar - elementar funksiyalar ailəsindəndir.Triqonometrik funksiyaların analoqu sayılır.Əsas Hiperbolik funksiyalar bunlardır:
Hiperbolik sinus
Hiperbolik kosinus
Hiperbolik tangens
Hiperbolik kotangens
Tərs Hiperbolik funksiyalar isə bunlardır:
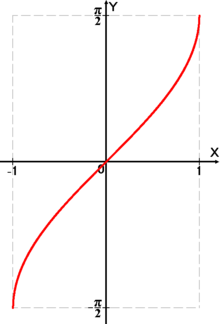
Hiperbolik arksinus
Hiperbolik arkskosinus
Hiperbolik arkstangens
Hiperbolik arkskotangens
== Riyazi hesablamalarda ==
Hiperbolik funksiyalar aşağıdakı funksiyalardan ibarətdir:
Hiperbolik sinus:
sinh
x
=
e
x
−
e
−
x
2
=
e
2
x
−
1
2
e
x
{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}}
Hiperbolik kosinus:
cosh
x
=
e
x
+
e
−
x
2
=
e
2
x
+
1
2
e
x
{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}}
Hiperbolik tangens:
tanh
x
=
sinh
x
cosh
x
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
2
x
−
1
e
2
x
+
1
{\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}
Hiperbolik kotangens:
coth
x
=
cosh
x
sinh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
=
e
2
x
+
1
e
2
x
−
1
{\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}
Hiperbolik sekans:
sech
x
=
(
cosh
x
)
−
1
=
2
e
x
+
e
−
x
=
2
e
x
e
2
x
+
1
{\displaystyle \operatorname {sech} \,x=\left(\cosh x\right)^{-1}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}}
Hiperbolik kosekans:
csch
x
=
(
sinh
x
)
−
1
=
2
e
x
−
e
−
x
=
2
e
x
e
2
x
−
1
{\displaystyle \operatorname {csch} \,x=\left(\sinh x\right)^{-1}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}}
Hiperbolik funksiyalar xəyali vahid (i) dairəsi ilə aşağıdakı kimi də ifade edilir:
Hiperbolik sinus:
sinh
x
=
−
i
sin
i
x
{\displaystyle \sinh x=-{\rm {i}}\sin {\rm {i}}x\!}
Hiperbolik kosinus:
cosh
x
=
cos
i
x
{\displaystyle \cosh x=\cos {\rm {i}}x\!}
Hiperbolik tangens:
tanh
x
=
−
i
tan
i
x
{\displaystyle \tanh x=-{\rm {i}}\tan {\rm {i}}x\!}
Hiperbolik kotangens:
coth
x
=
i
cot
i
x
{\displaystyle \coth x={\rm {i}}\cot {\rm {i}}x\!}
Hiperbolik sekans:
sech
x
=
sec
i
x
{\displaystyle \operatorname {sech} \,x=\sec {{\rm {i}}x}\!}
Hiperbolik kosekans:
csch
x
=
i
csc
i
x
{\displaystyle \operatorname {csch} \,x={\rm {i}}\,\csc \,{\rm {i}}x\!}
i, i2 = −1 - xəyali vahiddir.
== Hiperbolik funksiyaların törəmələri ==
d
d
x
sinh
x
=
cosh
x
{\displaystyle {\frac {d}{dx}}\sinh x=\cosh x\,}
d
d
x
cosh
x
=
sinh
x
{\displaystyle {\frac {d}{dx}}\cosh x=\sinh x\,}
d
d
x
tanh
x
=
1
−
tanh
2
x
=
sech
2
x
=
1
/
cosh
2
x
{\displaystyle {\frac {d}{dx}}\tanh x=1-\tanh ^{2}x={\hbox{sech}}^{2}x=1/\cosh ^{2}x\,}
d
d
x
coth
x
=
1
−
coth
2
x
=
−
csch
2
x
=
−
1
/
sinh
2
x
{\displaystyle {\frac {d}{dx}}\coth x=1-\coth ^{2}x=-{\hbox{csch}}^{2}x=-1/\sinh ^{2}x\,}
d
d
x
csch
x
=
−
coth
x
csch
x
{\displaystyle {\frac {d}{dx}}\ {\hbox{csch}}\,x=-\coth x\ {\hbox{csch}}\,x\,}
d
d
x
sech
x
=
−
tanh
x
sech
x
{\displaystyle {\frac {d}{dx}}\ {\hbox{sech}}\,x=-\tanh x\ {\hbox{sech}}\,x\,}
d
d
x
arsinh
x
=
1
x
2
+
1
{\displaystyle {\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}}
d
d
x
arcosh
x
=
1
x
2
−
1
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}}
d
d
x
artanh
x
=
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}}
d
d
x
arcsch
x
=
−
1
|
x
|
1
+
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{\left|x\right|{\sqrt {1+x^{2}}}}}}
d
d
x
arsech
x
=
−
1
x
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}
d
d
x
arcoth
x
=
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}}
== Hiperbolik funksiyaların inteqralları ==
∫
sinh
a
x
d
x
=
a
−
1
cosh
a
x
+
C
{\displaystyle \int \sinh ax\,dx=a^{-1}\cosh ax+C}
∫
cosh
a
x
d
x
=
a
−
1
sinh
a
x
+
C
{\displaystyle \int \cosh ax\,dx=a^{-1}\sinh ax+C}
∫
tanh
a
x
d
x
=
a
−
1
ln
(
cosh
a
x
)
+
C
{\displaystyle \int \tanh ax\,dx=a^{-1}\ln(\cosh ax)+C}
∫
coth
a
x
d
x
=
a
−
1
ln
(
sinh
a
x
)
+
C
{\displaystyle \int \coth ax\,dx=a^{-1}\ln(\sinh ax)+C}
∫
d
u
a
2
+
u
2
=
sinh
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{\sqrt {a^{2}+u^{2}}}}=\sinh ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
u
2
−
a
2
=
cosh
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{\sqrt {u^{2}-a^{2}}}}=\cosh ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
a
2
−
u
2
=
a
−
1
tanh
−
1
(
u
a
)
+
C
;
u
2
<
a
2
{\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\tanh ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}<a^{2}}
∫
d
u
a
2
−
u
2
=
a
−
1
coth
−
1
(
u
a
)
+
C
;
u
2
>
a
2
{\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\coth ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}>a^{2}}
∫
d
u
u
a
2
−
u
2
=
−
a
−
1
sech
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{u{\sqrt {a^{2}-u^{2}}}}}=-a^{-1}\operatorname {sech} ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
u
a
2
+
u
2
=
−
a
−
1
csch
−
1
|
u
a
|
+
C
{\displaystyle \int {\frac {du}{u{\sqrt {a^{2}+u^{2}}}}}=-a^{-1}\operatorname {csch} ^{-1}\left|{\frac {u}{a}}\right|+C}
C sabit ədəddir.
== Loqarifmaaltı tərs hiperbolik funksiyalar ==
arsinh
x
=
ln
(
x
+
x
2
+
1
)
{\displaystyle \operatorname {arsinh} \,x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}
arcosh
x
=
ln
(
x
+
x
2
−
1
)
;
x
≥
1
{\displaystyle \operatorname {arcosh} \,x=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1}
artanh
x
=
1
2
ln
1
+
x
1
−
x
;
|
x
|
<
1
{\displaystyle \operatorname {artanh} \,x={\tfrac {1}{2}}\ln {\frac {1+x}{1-x}};\left|x\right|<1}
arcoth
x
=
1
2
ln
x
+
1
x
−
1
;
|
x
|
>
1
{\displaystyle \operatorname {arcoth} \,x={\tfrac {1}{2}}\ln {\frac {x+1}{x-1}};\left|x\right|>1}
arsech
x
=
ln
1
+
1
−
x
2
x
;
0
<
x
≤
1
{\displaystyle \operatorname {arsech} \,x=\ln {\frac {1+{\sqrt {1-x^{2}}}}{x}};0<x\leq 1}
arcsch
x
=
ln
(
1
x
+
1
+
x
2
|
x
|
)
{\displaystyle \operatorname {arcsch} \,x=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1+x^{2}}}{\left|x\right|}}\right)}
== Teylor ardıcıllığı üçün hiperbolik funksiyalar ==
sinh
x
=
x
+
x
3
3
!
+
x
5
5
!
+
x
7
7
!
+
⋯
=
∑
n
=
0
∞
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}
cosh
x
=
1
+
x
2
2
!
+
x
4
4
!
+
x
6
6
!
+
⋯
=
∑
n
=
0
∞
x
2
n
(
2
n
)
!