Potensial Tələb

Tələb (ing. demand) — istehlakçıların müəyyən bir qiymətə və müddətdə məhsulu hansı miqdarda almağa hazır və imkanı olduğunu göstərir. Qrafikdə tələb əyri kimi ifadə olunur, və əsasən qiymətdən mənfi və ya tərs şəkildə asılıdır. Bu asılılıq tələbin qanununa müvafiqdir: bütün digər şərtlər dəyişməyən halda, qiymətin artımı tələbin düşməsinə səbəb olur. Bu qanun istehlakçıların seçimi üzrə müşahidələrə və sağlam və rasional düşüncələrə uyğun gəlir. Yüksək qiymət nə isə almağa niyyətini azaldır, və pərakəndə ticarətdə baş verən güzəştlər və satışlar müştəriləri cəlb etmək məqsədini daşıyırlar. Bundan başqa, hər bir yeni məhsul istehlakçıya azalan əlavə fayda gətirir. Misal üçün, ikinci yeyilən dönər daha az fayda gətirir, nəinki birinci. Ona görə əlavə məhsulu almağa daha aşağı qiymət səbəb ola bilər. Qiymətin dəyişməsi həm də sərvət və əvəz etmə effektlərinə yol verə bilər.

Potensial enerji termini ilk dəfə Şotland mühəndisi və fiziki Villiam Renkin tərəfindən XIX əsrdə elmə daxil edilmişdir. Potensial enerji U-maddi cismin konservativ qüvvələr sahəsində yerləşməsi hesabına iş görmə qabiliyyətini xarakterizə edən skalyar fiziki kəmiyyətdir. BS-də enerjinin ölçü vahidi Coul qəbul edilmişdir. Yerin cazibə sahəsində Ep aşağıdakı düsturla hesablanır: E p = m g → h {\displaystyle \mathrm {Ep=m{\vec {g}}h} } m- cismin kütləsi, g- sərbəst düşmə təcili, h- şərti qəbul edilmiş sıfır səviyyəsindən cismin ağırlıq mərkəzinə qədər olan hündürlükdür.

Termodinamik potensial — termodinamik sistemlərdə prosesləri izah etmək üçün istifadə olunan skalyar kəmiyyətlərdir. 1866-cı ildə fransız alimi Pyer Dühem tərəfindən elmə gətirilmişdir. ABŞ alimi Cozayya Uillard Gibbs elmi işlərində bir sıra termodinamik potensiallar göstərmişdir. Daxili enerji, entalpiya, Helmholts enerjisi, Hibbs enerjisi, Böyük terodinamik potensial, əlaqəli enerji kimi kəmiyyətlər termodinamik potensiallardır.

Riyazi fizikada skalyar potensial, sadəcə olaraq, iki fərqli mövqedə olan cismin potensial enerjilərindəki fərqin obyektin bir mövqedən digərinə keçdiyi yoldan deyil, yalnız mövqelərdən asılı olduğu vəziyyəti təsvir edir. Bu, üç fəzada olan skalyar sahədir və yalnız yerindən asılıdır. Tanış bir nümunə kimi: cazibə qüvvəsi səbəbindən potensial enerjini misal çəkmək olar. Skayar potensial vektor analizində və fizikasında əsas anlayışdır. Skalar potensial skalyar sahəyə misaldır. F vektor sahəsini nəzərə alaraq, P skalar potensialı belə müəyyən edilir ki: F = − ∇ P = − ( ∂ P ∂ x , ∂ P ∂ y , ∂ P ∂ z ) , {\displaystyle \mathbf {F} =-\nabla P=-\left({\frac {\partial P}{\partial x}},{\frac {\partial P}{\partial y}},{\frac {\partial P}{\partial z}}\right),} burada, ∇P P -nin qradiyentidir və tənliyin ikinci hissəsi x, y, z Dekart koordinatlarının funksiyası üçün mənfi gradientdir. Bəzi hallarda riyaziyyatçılar potensialı müəyyən etmək üçün qradientin qarşısında müsbət işarədən istifadə edə bilərlər. Qradient baxımından P nin bu tərifinə görə, hər hansı bir nöqtədə F istiqaməti o nöqtədə P -nin ən kəskin azalmasının istiqamətidir, onun böyüklüyü vahid uzunluğa düşən azalmanın sürətidir. F yalnız skalyar potensial baxımından təsvir edilməsi üçün aşağıdakı ekvivalent ifadələrdən hər hansı biri doğru olmalıdır: − ∫ a b F ⋅ d l = P ( b ) − P ( a ) , {\displaystyle -\int _{a}^{b}\mathbf {F} \cdot d\mathbf {l} =P(\mathbf {b} )-P(\mathbf {a} ),} burada inteqrasiya a yerindən b yerinə keçən İordan qövsü üzərindədir və P ( b P(b) P qiymətləndirilir. ∮ F ⋅ d l = 0 , {\displaystyle \oint \mathbf {F} \cdot d\mathbf {l} =0,} burada, inteqral hər hansı sadə qapalı yolun üzərindədir, əks halda İordan əyrisi kimi tanınır.

Effektiv tələb bazarda — başqa bir bazarda alıcılar məhdudlaşdırıldıqda ortaya çıxan məhsul və ya xidmətə olan tələbdir. Alıcılar başqa bir bazarda məhdudlaşmadığı zaman meydana gələn şərti tələblə ziddiyyət təşkil edir. Bütövlükdə mallar üçün məcmu bazarda şərti və ya effektiv olan tələb məcmu tələb adlanır. Səmərəli təklif anlayışı effektiv tələb anlayışına bənzəyir. Bazarlar daima tarazlıq qiymətlərini saxlamadıqda təsirli tələb və ya təklif konsepsiyası aktualdır. Nümunə olaraq əmək bazarından əmtəə bazarına axını vurğulamaq olar. Əmək bazarında əgər tarazlıq varsa və insanlar təklif etmək istədikləri bütün əməyi təmin edə bilmirlərsə, təklif edə biləcəkləri məbləğ mallara olan tələblərinə təsir edəcək; tədarük edilə bilən əmək miqdarının məhdudlaşdırılması şərtilə mallara olan tələb, onların mallara olan təsiridir. Əksinə, əmək bazarında balanssızlıqlar olmasaydı, fərdlər eyni vaxtda həm tədarük etmək üçün əməyin miqdarını, həm də alacaq malların miqdarını seçər, ikincisi isə mallara olan şərti ehtiyacları olardı. Bu nümunədə mallara təsirli tələb mallara olan şərti tələbdən az olacaqdır. Əksinə, mal bazarında çatışmazlıq olarsa, insanlar əmək bazarında tarazlıq olsaydı, olduğundan daha az əmək sərf etməyi (və daha çox boş vaxt keçirməyi) seçə bilərlər.

Məcmu tələb əyrisi açıq bir iqtisadiyyatda bütün xərclərin cəmi kimi ifadə edilir: AD= C+I+G+NX C- istehlak xərcləri; I- investisiyalar; G- dövlət xərcləri; NX- xalis ixrac, (NX= İxrac - İdxal). Bu halda AD əyrisi hər qiymət səviyyəsində ev təsərrüfatlarının, firmaları və dövlətin almaq istədiyi əmtəə və xidmətlərin həcmini əks etdirəcək. Başqa sözlə, AD əyrisi yuxarıda göstərilən bütün istehlak, investisiya, xalis ixrac və dövlət xərclərini təmsil edir. AD əyrisindəki dəyişmələrə səbəb ola biləcək amillər 3 qrupda əks olunur: Gözlənmələr; Xaricilərin gəlirləri və valyuta kursu; Dövlət siyasəti. Ev təsərrüfatları gələcəkdə gəlirlərində artım gözləyirlərsə, daha çox istehlak edəcəklər. Bu məcmu tələbin artmasına gətirib çıxaracaq və AD əyrisi sağa sürüşəcək. Bunun əksi olaraq gəlirlərin azalması gözlənilirsə, AD əyrisi sola doğru hərəkət edəcək. Bu hal firmalara da aiddir. Belə ki, firmalar gələcəkdə iqtisadiyyatda canlanma gözləyirlərsə, investisiya yönümlü xərclərini artıracaqlar. Bu məcmu tələbdə artışa və AD əyrisinin sağa doğru irəlləməsinə səbəb olacaq.

Tələb zəmanəti (fr. garantie autonome) — fransız mülki hüququnda muxtar zəmanət, öhdəliklərin yerinə yetirilməsi üçün üç növ şəxsi təhlükəsizlik növündən biridir. Bu zəmanət sayəsində zamin şəxs üçüncü bir şəxsin üzərinə götürdüyü öhdəliyi nəzərə alaraq ya kreditorun ilk tələbi ilə, ya da müqavilədə nəzərdə tutulmuş başqa bir qaydada müəyyən miqdarda pul ödəmək öhdəliyini götürür. Öhdəliklərin yerinə yetirilməsi üçün şəxsi təhlükəsizliyin digər iki növü zaminlik (xəbərdarlıq) və niyyət memorandumudur (lettre d’intention). Hər hansı digər zəmanət kimi, muxtar bir zəmanət də borclunun öz öhdəliklərini yerinə yetirməsini təmin etmək üçün hazırlanmışdır. Bununla birlikdə, bu zəmanət, zəmanətçinin onlara zəmanət verilmiş öhdəliklə bağlı hər hansı bir etiraz bildirmək hüququna malik olmadığı xüsusiyyətinə malikdir. Bundan əlavə, zaminin borclunun əmlakından əvvəl borc götürülməsini (bénéfice de discussion) və ya öhdəliyinin bölüşdürülməsini (bénéfice de division) kreditordan tələb etməsinə icazə vermir. Əksinə bir razılaşma olmadığı təqdirdə, muxtar zəmanətlə müəyyən edilmiş təminat, zəmanət verilmiş öhdəliyə əməl etmir, çünki təbiətinə görə yalnız şəxsi və daşınmaz əmlakla təmin olunur. Benefisiar (faydalanan) tərəfindən aşkar şəkildə sui-istifadə (dələduzluq) və ya saxtakarlıq və ya tələb irəli sürən şəxslə sövdələşmə halında, zamin onun öhdəliyi ilə bağlı deyildir. Fransız qanunlarındakı xüsusi müddəalara əsasən, muxtar zəmanət miras hüququnda da istifadə olunur.

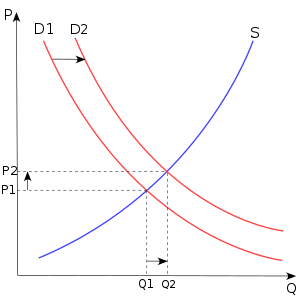
Tələb şoku iqtisadiyyatda (ing. demand shock) — mallara və ya xidmətlərə tələbi müvəqqəti artıran və ya azaldan qəfil bir hadisədir. Müsbət tələb şoku ümumi tələbi (ÜM) artırır və mənfi tələb şoku ümumi tələbi azaldır. Malların və xidmətlərin qiymətləri hər iki halda da təsir göstərir. Mallara və ya xidmətlərə tələb artdıqda, tələb əyrisinin sağa doğru dəyişməsi səbəbindən qiymətləri (və ya qiymət səviyyəsi) artır. Tələb azaldıqda, tələb əyrisinin sola doğru dəyişməsi səbəbindən qiyməti azalır. Tələb şokları vergi dərəcələri, pul təklifi və dövlət xərcləri kimi şeylərdə baş verə bilər. Məsələn, vergi ödəyiciləri vergi endirimlərindən sonra hökumətə daha az borc verirlər, beləliklə şəxsi xərcləri üçün daha çox pul azad edirlər. Vergi ödəyiciləri mal və xidmətlər almaq üçün puldan istifadə etdikdə qiymətləri qalxır. 2002-ci ilin noyabr ayında İngiltərədəki əlverişsiz iqtisadi vəziyyətin ortasında İngiltərə Bankının direktoru Mervin Kinq, daxili iqtisadiyyatın yaxın gələcəkdə "güclü mənfi tələb şokuna" səbəb ola biləcəyi qədər balanssız olduğunu xəbərdar etdi.

Mikroiqtisadiyyatda istehlakçının Hiks tələbinə müvafiqliyi ona təyin edilmiş fayda gətirən və xərclərini minimallaşdıran məhsulların dəstəsinə tələbi bildirir. Əgər bu müvafiqlik müəyyən bir funksiyadır, onda ona Hiks tələb funksiyası, və ya əvəzini verən tələb funksiyası deyilir. Funksiya Con Hiks (John Hicks) şərəfinə adlandırılmışdır. Riyazi şəkildə: h ( p , u ¯ ) = arg ⁡ min x ∑ i p i x i {\displaystyle h(p,{\bar {u}})=\arg \min _{x}\sum _{i}p_{i}x_{i}} s u c h t h a t u ( x ) ≥ u ¯ {\displaystyle {\rm {such\ that}}\ \ u(x)\geq {\bar {u}}} Harda ki h(p,u) Hiks tələb funksiyasıdır, və ya tələb olunan məhsul dəstəsidir, p qiymətləri səviyyəsidir, və u ¯ {\displaystyle {\bar {u}}} faydadır. Burda p qiymətlərin vektorudur, və X tələb olunan miqdarların vektorudur. Deməli bütün pixi cəmi X məhsullarına gedən ümumi xərcdir. Hiks tələb funksiyaları riyazi hesablarda işlətmək asandır çünki onlar gəlirin olduğunu tələb etmirlər. Əlavə olaraq, minimallaşdırılmış olmalı funksiya x i {\displaystyle x_{i}} üzrə xəttidir, və bu optimizasiya problemini asanlaşdırır. Amma verilmiş p qiymətləri və w {\displaystyle w} gəliri ilə tələbi təsvir edən x ( p , w ) {\displaystyle x(p,w)} Marşal tələb funksiyasını birbaşa müşahidə etmək daha asandır. Hər ikisi bir biri ilə adi şəkildə əlaqədədir: h ( p , u ) = x ( p , e ( p , u ) ) , {\displaystyle h(p,u)=x(p,e(p,u)),\ } Harda e ( p , u ) {\displaystyle e(p,u)} məxaric funksiyasıdır (verilmiş fayda əldə etmək üçün minimal gəliri göstərən funksiya) h ( p , v ( p , w ) ) = x ( p , w ) , {\displaystyle h(p,v(p,w))=x(p,w),\ } Harda v ( p , w ) {\displaystyle v(p,w)} vasitəli fayda funksiyasıdır (verilmiş qiymətlər və müəyyən gəlir ilə əldə edilən faydanı göstərən funksiya).

Mikroiqtisadiyyatda istifadə olunan Marşal tələb funksiyası (ing. Marshallian demand function) (Alfred Marşal şərəfinə) göstərir ki, istehlakçı hər bir qiymət və var-dövlət vəziyyətində nə qədər alacaq, nəzərə alaraq ki bu qərar faydanın maksimallaşdırılmasının problemini həll edəcək. Marşal tələb funksiyası həm də Valras tələbi (Leon Valrasın şərəfinə) və ya "əvəzini verməyən tələb funksiyası" kimi tanınır, çünki Marşalın ilkin təhlili var-dövlətin effektlərini nəzərə almırdı. Faydanın maksimallaşdırılması probleminə uyğun olaraq, p qiymətlərinə L məhsullar var. w var-dövlətinə malik olan istehlakçı və bir sıra imkanı çatan seçimlər mövcüddur: B ( p , w ) = { x : ⟨ p , x ⟩ ≤ w } {\displaystyle B(p,w)=\{x:\langle p,x\rangle \leq w\}} , burada, ⟨ p , x ⟩ {\displaystyle \langle p,x\rangle } qiymətlərin daxili məhsul fəzası və məhsulların sayıdır. İstehlakçının faydalılıq düsturu aşağıdakı kimidir: u : R + L → R {\displaystyle u:{\textbf {R}}_{+}^{L}\rightarrow {\textbf {R}}} . İstehlakçının Marşal tələb müvafiqliyi belə təyin olunur: x ∗ ( p , w ) = argmax x ∈ B ( p , w ) ⁡ u ( x ) {\displaystyle x^{*}(p,w)=\operatorname {argmax} _{x\in B(p,w)}u(x)} . Əgər faydanı maksimallaşdıran seçim hər bir qiymət və var-dövlət üçün yeganədirsə, bu Marşal tələb funksiyası adlanır. Əgər iki məhsul varsa, onda öz gəlirini həmişə hər bir məhsul üçün yarıya bölən istehlakçı Marşal tələb funksiyasına malikdir. x ( p 1 , p 2 , w ) = ( w 2 p 1 , w 2 p 2 ) .

Sınıq tələb əyrisi oliqopoliya və inhisarçı rəqabətlə bağlı iqtisadi nəzəriyyə və oliqopoliya bazar modelidir. Sınıq tələb əyrisi oliqopol bazarda yapışqan qiymətlərin olma səbəbini izah edir. Firmalar eyni böyüklükdədir. Bircins mallar istehsal edirlər. Firmalar digər firmaların qiymət yüksəltməsinə etinasız, qiymət azaltmasına isə həssasdır. Bütün firmalar eyni qiymətdə təklif edirlər. MR əyrisi kəsikdir. Bu nəzəriyyə 1939-cu ildə Paul Sweezy tərəfindən irəli sürülmüşdür. O "Demand Under Conditions of Oligopoly" (Oliqopol şərtlər altında tələb) nəşrində bunu izah etmişdir. Klassik oliqopol bazar nəzəriyyəsinə görə bir əmtəənin qiyməti onun marjinal xərc və gəlirlərindən yüksək olur (P > MR = MC).

Son illərdə dünyada şəhər nəqliyyat sektorunda ənənəvi, böyük investisiyalar tələb edən və geri dönüşü mümkün olmayan nəqliyyat sisteminin inkişaf etdirilməsi siyasəti yerinə, daha az sərmayə tələb edən və əldə olan qaynaqların daha ağıllı və məhsuldar istifadə etməklə inkişaf etdirilmiş nəqliyyat siyasəti tətbiq edilir. İctimai nəqliyyat vasitələrinə olan artan tələbatı təşviq etmək yerinə bu tələbi idarə etmək üçün inkişaf etdirilmiş bir "Nəqliyyatda tələbin idarə edilməsi" siyasəti həyata keçirilir. Nəqliyyat və tıxac planlaması baxımından tələbin idarə edilməsi (Təklifin tələb yaratması) - ( ing. ing.Induced demand ) Dünyanın bir çox ölkələrinin əhalisinin artması, nəqliyyat vasitələri sayında, sərnişin və yük daşımacılığnda və bunlara əlavə olaraq qloballaşmanın sürətlə artması səfərlərə olan tələbə təsir etməkdədir. Bütün bu hadisələr insanların ev ilə iş yerləri arasında seçim etdikləri nəqliyyat imkanları və yük daşımacılığı seçənəklərini də dəyişdirir. Nəqliyyat ilə əlaqədar problemlər çox vaxt iqtisadi baxımdan yüksək xərclərə səbəb olur. Səfərlərə olan tələbin ödənilməsi, nəqliyyat (çatdırılma) və bununla əlaqədar imkanları (xərcləri) artırılmadan səfərlərə (yolculuğa) olan tələbi azaldaraq və yaxud məhdudlaşdıraraq həll etməyi qarşısına məqsəd qoyan planlamadır. Nəqliyyat problemlərini və tıxacların həll edilməsində böyük həcmli investisiyalar qoymadan aradan qaldırılması səfər vərdişlərinin dəyişdirilməsini hədəfləməkdədir. Bununla bərabər bütün nəqliyyat problemlərini və nəqliyyat tıxanıqlığının aradan qaldırılmasında hər dərdə dərman olamasa da olduqca təsirli bir strateji planlaşdırma hesab olunur. Nəqliyyat xidmətlərində ənənəvi olaraq təklif yönümlü həll istiqamətlərinə daha çox yer verilir və bu istiqamətdə nəqliyyatın imkanlarını (tutumunu, həcmini) artıracaq işlər görülür.

Tələb və təklif (ərəb. طلب و تکلیف‎, ing. Demand and supply, rus. Спрос и предложение) —iqtisadiyyatda ən əsas anlayışlardan biridir. Bu model tələb və təklifin qiymətə necə dəyişildiyini və bazarda müvazinətin əmələ gəlməsini göstərir. Mikroiqtisadiyyatda əsasən bir müəyyən məhsul bazarı araşdırılır, makroiqtisadiyyatda isə bütun məhsullar üzrə ümumi tələb və təklif nəzərə alınır. Tələb istehlakçıların müəyyən bir qiymətə və müddətdə məhsulu hansı miqdarda almağa hazır və imkanı olduğunu göstərir. Qrafikdə tələb əyri kimi ifadə olunur, və əsasən qiymətdən mənfi və ya tərs şəkildə asılıdır. Tələb əyrisi – əmtənin qiyməti ilə ona olan tələbin həcmi arasındakı əlaqəni əks etdirən əyridir. Bu asılılıq tələbin qanununa müvafiqdir: bütün digər şərtlər dəyişməyən halda (ceteris paribus), qiymətin artımı tələbin düşməsinə səbəb olur.

AD-AS modeli makroiqtisadiyyatı başa düşmək üçün yaradılan standard dərslik modelidir. Bu model Məcmu Tələbin Məcmu Təklifə bərabər olduğu haldakı qiymət səviyyəsini və real istehsal həcmini göstərir. Məcmu tələb əyrisi aşağı meyillidir. Bu da aşağı qiymət səviyyəsində istehsala daha çox tələb olmasını göstərir. Məcmu tələbin aşağı meylli olmasına 3 effekt təsir göstərir: Piqu və ya real balans effekti. Əgər ölkədə real qiymətlərin səviyyəsi aşağı enirsə, real sərvət artır. Yəni, qiymətlər enirsə alıcı 1 manatla daha çox məhsul ala bilir, bu da məcmu tələbi artırır. Keyns və ya faiz dərəcəsi effekti. Məhsulların qiyməti düşürsə, pula olan tələb azalır. Bu faiz dərəcəsini aşağı endirir.