
Endosimbiyoz qaydası
'Endosimbiyoz qaydası' , eukariot hüceyrə orqanoid lərindən mitoxondri və plastit lərin mənşəyi ilə məşğul olur. Qayda söz mövzusu orqanoidlərin eukariot hüceyrələrlə birlikdə yaşamağa başlayan nüvəsinə canlı lardan mənşə aldığını irəli sürər. Mitoxondri, proteobakterilerden, kloroplast lar isə siyanobakteri lərdən inkişaf etmişdir.
1883-ci ildə Alman botanik Andreas Schimper işlərində yaşıl bitki lərdəki kloroplastların siyanobakterilerle bənzərliklər göstərdiyini müşahidə və yaşıl bitkilərin iki orqanizmin simbiyoz həyatından ortaya çıxdığını düşünmüşdü. Rus botanik Konstantin Mereschkowski bu işlərdən xəbərdar və 1905-ci ildə ilk dəfə endosimbiyoz nəzəriyyədən açıqca bəhs etmişdir. 1920-ci illərdə mitoxondrilərin endosimbiyotik keçmişi haqqındakı düşüncüler Ivan Wallin tərəfindən geliştirlmeye davam etdi. Başlanğıcda bu fərziyyələr nəzərə alınmadı.1960'larda elektron mikroskoplarıyla edilən koloroplastların və siyanobkaterilerin daha ətraflı müqayisələri və plastitlerin və mitoxondrilərin öz DNT 'larının olduğu kəşfi köhnə fikirlərin yenidən doğuşuna səbəb oldu.
Endosimbiyoz fərziyyəsi Lynn Margulis tərəfindən yaradılmış və ondan sonra məşhurluq qazanmışdır. 1981-ci il tarixli Hüceyrə təkamülündə Ortaq Həyat (Symbiosis in Cell Evolution) adlı işində eukariot hüceyrələr mənşəyinin birlikdə yaşayan primitiv prokrayot canlı birliklərinə dayandığını müdafiə etmişdir.
Lynn Margulis və Dorion Sagan'a görə "həyat dünyanı döyüşlə deyil dayanışmayla fəth etmişdir və Darvin 'in təbii seçilim e söykənən təkamül tezisi əskikdir".
Lopital qaydası
Lopital qaydası (teoremi) (həmçinin Bernulli — Lopital qaydası ) — funksiyaların limitinin tapılması metodudur. Bu metod ən çox
0
/
0
{\displaystyle 0/0}
və
∞
/
∞
{\displaystyle \infty /\infty }
qeyri-müəyyənliklərinin tapılmasında istifadə olunur. Metodu əsaslandıran teorem iddia edir ki, bəzi şərtlərdə funksiyaların əlaqəsinin limiti onların törəmələri limitinə bərabərdir.
Lopital teoremi:
lim
x
→
a
f
(
x
)
=
lim
x
→
a
g
(
x
)
=
0
v
e
-
y
a
∞
{\displaystyle \lim _{x\to a}{f(x)}=\lim _{x\to a}{g(x)}=0\operatorname {ve-ya} \infty }
;
f
(
x
)
{\displaystyle ~f(x)}
və
g
(
x
)
{\displaystyle ~g(x)}
---
a
{\displaystyle ~a}
ətrafında differensiallaşdırır;
g
′
(
x
)
≠
0
{\displaystyle g'(x)\neq 0}
---
a
{\displaystyle ~a}
-nın ətrafında təyin olunur;
lim
x
→
a
f
′
(
x
)
g
′
(
x
)
{\displaystyle \lim _{x\to a}{\frac {f'(x)}{g'(x)}}}
olur,
onda
lim
x
→
a
f
(
x
)
g
(
x
)
=
lim
x
→
a
f
′
(
x
)
g
′
(
x
)
{\displaystyle \lim _{x\to a}{\frac {f(x)}{g(x)}}=\lim _{x\to a}{\frac {f'(x)}{g'(x)}}}
olar.
Limitlər həmçinin birtərəfli ola bilər.
Qeyri-müəyyənliklərin bu cür açılış üsulu 1696-cı ildə müəllifi Giyom Lopital olan "Analyse des Infiniment Petits" dərsliyində dərc edilmişdi. Metodu ilk kəşf edən İohan Bernulli məktubunda Lopitala bu haqda bildirmişdi.
Sahə qaydası
Sahə qaydası — təyyarələrin dizaynındakı bir qaydadır, bu səsə yaxın və ya supersonik sürətində dalğa müqavimətini azaltmağa imkan verir. Bu sürət aralığı müasir mülki və hərbi təyyarələr arasında ən çox istifadə olunur.
Səsə yaxın uçuş sürətində hava axınının yerli sürəti, axının təyyarənin struktur elementləri ətrafında getdiyi yerlərdə, səs sürətinə çata bilər. Bu davranışın müşahidə olunduğu sürətin dəyəri təyyarənin dizaynından asılı olaraq dəyişir və kritik Max sayı adlanır. Belə yerlərdə yaranan şok dalğaları güclü sürətlə böyüyən bir müqavimətə malikdir. Bu müqavimət dalğa müqaviməti adlanır. Zərbə dalğalarının gücünü azaltmaq üçün təyyarənin kəsişmə sahəsi təyyarənin gövdəsi boyunca mümkün qədər rəvan şəkildə dəyişməlidir.
Sahə qaydasında deyilir ki, kəsişən ərazinin eyni uzunlamasına paylanması olan iki təyyarə, bu sahənin eninə füzelyaj istiqamətində paylanmasından asılı olmayaraq eyni dalğa empedansına malikdir (yəni, füzelyajın özündə və ya qanadlarında). Üstəlik, güclü şok dalğalarının meydana gəlməməsi üçün bu paylama hamar olmalıdır. Bu qaydanın tətbiq edilməsinə bir nümunə, təyyarənin qaynaq hissəsinin qanadlarla qovşağında enməsi, kəsişən sahənin dəyişməməsi.

1% qaydası
1% qaydası — internet mədəniyyətində internet icması daxilində iştirakla bağlı ümumi qayda. Qaydada qeyd olunur ki, veb-sayt istifadəçilərinin yalnız 1%-i aktiv şəkildə yeni məzmun yaradır, qalan 99%-i isə sadəcə lurkerlik edir. Variantlara 1–9–90 qaydası (bəzən 90–9–1 prinsipi və ya 89:10:1 nisbəti adlanır) daxildir. Burada viki kimi birgə yaradılan veb-saytda icma iştirakçılarının 90%-nin yalnız məzmunu istehlak etdiyi, 9%-nin məzmunu dəyişdirdiyi və ya yenilədiyi, 1%-nin isə məzmun əlavə etdiyi qeyd olunur.
Oxşar qaydalar informasiya elmində də məlumdur. Məsələn, Pareto prinsipi kimi tanınan 80/20 qaydası fəaliyyətin necə müəyyən edilməsindən asılı olmayaraq, qrupun 20 faizinin fəaliyyətin 80 faizini istehsal edəcəyini bildirir.
1% qaydasına əsasən, internet istifadəçilərinin təxminən 1%-i məzmun yaradır, 99%-i isə sadəcə həmin məzmunun istehlakçısıdır. Məsələn, bir forumda yazı yazan hər bir şəxsə qarşılıq təxminən 99 nəfər həmin foruma baxır, lakin mesaj yazmır. Bu termin müəllif və bloqqerlər Ben MakKonnell və Ceki Huba tərəfindən icad edilmişdir, baxmayaraq ki, əvvəllər eyni konsepsiyaya istinadlar bu addan istifadə etməmişdir.
Onlayn fəaliyyətə istinad edərək, lurker termini internet icmasında başqaları ilə əlaqədə olmayan onlayn müşahidəçiyə istinad etmək üçün istifadə olunur.

Oktet qaydası
Oktet qaydası (oktet nəzəriyyəsi) — kovalent kimyəvi rabitələrin əmələ gəlməsinin səbəblərini izah etmək üçün G. N.Lyuis tərəfindən təklif edilmişdir. Bu qaydaya görə, molekullar əmələ gəldikdə, atomlar valentlik elektronlarını cüt-cüt paylaşaraq nəcib qazların elektron konfiqurasiyasına bənzər 8 elektron valentlik qabığına nail olmaq ehtiyacını ödəyirlər. Lyuisin bu fundamental kəşfi əhəmiyyətinə görə Elementlərin Dövri Qanunu və üzvi birləşmələrin quruluş nəzəriyyəsi kimi kəşflərlə eyni səviyyədədir. Oktet qaydasının yalnız məhdud sayda hallarda mövcud olduğuna dair geniş yayılmış inam, Elementlərin Dövri Qanununun universal olmadığı iddiası qədər yanlışdır. Oktet qaydasına "uyğunsuzluğun" bütün nümunələrini aşağıdakı üç qrupa bölmək olar:
thumb
Molekulu əmələ gətirən atomların valentlik elektronlarının cəmi təkdir. Buna misal olaraq, azot oksidi NO molekulunu göstərmək olar.
Bu zaman azot atomunun (5) və oksigenin (6) valentlik elektronlarının cəmi 11-dir, ona görə də bu molekulda oksigen atomu səkkiz elektron qabığa çatır, azot atomu isə çatmır. Bu halda hər iki atomun səkkiz elektron qabığa çatması ilkin olaraq qeyri-mümkündür. Azot atomunun elektron qabığını doldurmaq istəyi bu molekulun kimyəvi reaktivliyini izah edir.
Molekul üçmərkəzli rabitələr hesabına əmələ gəlir, məsələn, KI3.

Texniki
Texnologiya ("sənət haqqında bilik", Yunanca: τέχνη, techne, "sənət, bacarıq, əl hiyləsi"; və -λογία, -logia - bilik, elm ) — malların və ya xidmətlərin istehsalında və ya elmi tədqiqat kimi məqsədlərin həyata keçirilməsində istifadə olunan hər hansı texnika, bacarıq, üsul və proseslərin məcmusudur. Bu nöqteyi-nəzərdən kompüter texnologiyası baxılan sahədə kompüter texnikasının aparat və proqram vasitələrindən istifadə texnologiyası deməkdir.
Texnologiyanın ən sadə forması əsas alətlərin işlənib hazırlanması və istifadəsidir. Formalı daş alətlərin tarixdən əvvəlki ixtirası və ardınca yanğını idarə etmək üsullarının kəşfi qida mənbələrini artırdı. Sonrakı Neolit inqilabı bunu genişləndirdi və bir ərazidən əldə edilən ruzi dörd qat artırdı. Təkərin ixtirası insanlara səyahət etmək və ətraf mühiti idarə etməkdə kömək etdi.
Tarixi dövrlərdə, o cümlədən mətbəə, telefon və internetdə baş verən inkişaflar ünsiyyət üçün fiziki maneələri azaldıb və insanların qlobal miqyasda sərbəst şəkildə qarşılıqlı əlaqədə olmasına imkan verib.
Texnologiyanın çoxlu təsirləri var. Bu, daha qabaqcıl iqtisadiyyatların (o cümlədən, bugünkü qlobal iqtisadiyyatın) inkişafına kömək etdi və asudə vaxt sinfinin yüksəlməsinə imkan verdi. Bir çox texnoloji proseslər çirklənmə kimi tanınan arzuolunmaz əlavə məhsullar əmələ gətirir və təbii ehtiyatları Yerin ətraf mühitinə ziyan vuraraq tükəndirir.
Təhlükəsizlik
Təhlükəsizlik — təhlükənin minimal olduğu bir vəziyyət.
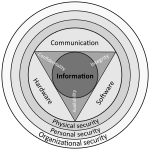
İnformasiya (Kəşfiyyat) təhlükəsizliyi: İnformasiya təhlükəsizliyi, yazılı, şifahi və ya elektron mediada məlumatların qorunması və doğru məlumatların doğru zamanda lazımi şəxsə çatdırılması ilə əlaqədardır.
İnformasiya texnologiyaları təhlükəsizliyi: İnformasiya cihazları və proqram təminatlarının istifadəsi nəticəsində yarana biləcək risk və təhlükələri araşdıran informasiya texnologiyaları şöbəsi.
Fiziki təhlükəsizlik: Fiziki təhlükəsizlik təcavüzkarların bir qurğu, qaynaq və ya fiziki məlumat əldə etməsinin qarşısını almaq və ya yayındırmaq üçün görülən bir tədbirdir. İxtisaslı işçi qüvvəsindən belə işlərdə istifadə olunur.
Qida təhlükəsizliyi: İki konsepsiyanı özündə birləşdirir.
Beynəlxalq münasibətlər sahəsində insanlar aclıq və qıtlıq içində olmamalıdırlar.
Bu qidanın istehsal mərhələsindən son istehlakçıya çatana qədər insan sağlamlığı üçün uyğun şərtlərdə qida istehsalı, saxlanması, qablaşdırılması və daşınmasının təmin edilməsidir.
İnsan təhlükəsizliyi: Milli təhlükəsizlik, suverenlik və insan hüquqları sahəsində konseptual bir problemi göstərən beynəlxalq münasibətlər terminidir. Bunu insan hüquqları kimi də ifadə etmək olar.

Eynşteyn cəmləmə qaydası
Eynşteyn cəmləmə qaydası Albert Eynşteyn tərəfindən, Ümumi Nisbilik Nəzəriyyəsi yazılarkən daha qısa və anlaşıqlı dildə cəmləmə əməliyyatını(
∑
{\displaystyle \sum }
) ifadə etmək məqsədilə gətirilib. Sonralar bu nəzəriyyədən istifadə edən digər alimlər arasında da bu ifadə tərzi yayılmağa başladı.
Qayda ondan ibarətdir ki, hər hansı növ tenzorlardan, koordinatlardan ibarət birhədlidə eyni simvol həm alt indeks, həm də üst indeks kimi yazılırsa, bu, o birhədlidə həmin indeks üzrə bütün komponentlərin bir-birilə cəmlənməsi anlamına gəlir:
x
α
x
α
=
∑
α
=
0
m
x
α
x
α
{\displaystyle x^{\alpha }x_{\alpha }=\sum _{\alpha =0}^{m}{x^{\alpha }x_{\alpha }}}
Bu,
x
→
{\displaystyle {\vec {x}}}
yerdəyişmə vektoru üçün uzunluğun kvadratı(
|
x
→
|
2
{\displaystyle |{\vec {x}}|^{2}}
) düsturu olub,
x
α
{\displaystyle x^{\alpha }}
—
x
→
{\displaystyle {\vec {x}}}
yerdəyişmə vektorunun
α
{\displaystyle \alpha }
koordinatını,
x
α
{\displaystyle x_{\alpha }}
—
x
~
{\displaystyle {\tilde {x}}}
yerdəyişmə kovektorunun
α
{\displaystyle \alpha }
koordinatını(
x
α
=
g
α
λ
x
λ
{\displaystyle x_{\alpha }=g_{\alpha \lambda }x^{\lambda }}
),
m — koordinatların sayını göstərir.
İki
V
→
=
(
V
0
,
V
1
,
V
2
,
V
3
)
{\displaystyle {\vec {V}}=(V^{0},V^{1},V^{2},V^{3})}
və
U
→
=
(
U
0
,
U
1
,
U
2
,
U
3
)
{\displaystyle {\vec {U}}=(U^{0},U^{1},U^{2},U^{3})}
vektoru verilirsə bu vektorların skalyar hasili Eynşteyn cəmləmə qaydası ilə daha qısa şəkildə belə ifadə olunar:
V
→
⋅
U
→
=
V
α
U
α
=
V
0
U
0
+
V
1
U
1
+
V
2
U
2
+
V
3
U
3
,
U
α
=
g
α
λ
U
λ
{\displaystyle {\vec {V}}\cdot {\vec {U}}=V^{\alpha }U_{\alpha }=V^{0}U_{0}+V^{1}U_{1}+V^{2}U_{2}+V^{3}U_{3},\quad U_{\alpha }=g_{\alpha \lambda }U^{\lambda }}
burada
g
α
λ
{\displaystyle g_{\alpha \lambda }}
— metrik tenzordur. Evklid fəzasının metrikası diaqonal olduğundan və sıfırdan fərqli bütün komponentləri vahidə bərabər olduğundan(
g
α
β
=
δ
β
α
{\displaystyle g_{\alpha \beta }=\delta _{\beta }^{\alpha }}
) skalyar hasil
V
→
⋅
U
→
=
V
0
U
0
+
V
1
U
1
+
V
2
U
2
+
V
3
U
3
{\displaystyle {\vec {V}}\cdot {\vec {U}}=V^{0}U^{0}+V^{1}U^{1}+V^{2}U^{2}+V^{3}U^{3}}
formasını alır.

Hibbsin fazalar qaydası
Hibbsin fazalar qaydası — ilk dəfə fazalar qaydası adı ilə 1876-cı ildə amerika alimi V.Hibbs tərəfindən verilmişdi.
Tarazılıq halında olan sistemdə fazalar sayı (F), sərbəstlik dərəcəsi (S) və asılı olmayan komponentlər sayı (K) bir-biri ilə aşağıdakı sadə nisbət üzrə əlaqədardır:
S+F=K+2
asılılığından sərbəstlik dərəcəsinin sayı tapılarkən, komponentlər sayından fazalar sayı çıxılır və alınan fərqin üzərinə 2 gəlinir.
S=K-F+2
fazalar qaydasına əsasən sistemlərin komponentlər sayına, fazalar sayına və sərbəstlik dərəcəsi sayına görə müəyyən təsnifatı mövcuddur.
Birkomponentli sistem üçün (K=1) yuxarıda göstərilən bərabərlik belə şəkil alır:
S=3-F
fazalar sayı da bir olduqda sistem ikivariantlı, yəni sərbəstlik dərəcəsinin sayı 2-yə bərabər olur. Sərbəstlik
S=3–1=2 dərəcəsinin 2 olması o deməkdir ki, müəyyən həddə cictemin halını müəyyən edən parametrlərdən ikisi, məsələn təzyiq və temperatur dəyişdirilərsə, sistemin halı dəyişmir.
sistemdə fazalar sayı vahiddən az ola bilmədiyindən, birkomponenetli sistem bundan artıq sərbəstlik dərəcəsi sayına malik ola bilməz. Belə sistemə misal buz, maye, su və ya su buxarı ola bilər.
İki faza arasındakı tarazılıq halında sistem birvariantlıdır:
S=3–2=1
Bunun misalı buz↔su, su↔buxar və ya buz↔buxar sistemləri ola bikər.
Üç faza arasındakı tarazılıq halında sistem variantsızdır (nonvariantdır):
S=3–3=0 bu hala misal müvazinətdə olan buz↔su↔su buxarı ola bilər.
Sərbəstlik dərəcəsinin sıfra bərabər olması o deməkdir ki, sistemin heç bir parametri dəyişdirilə bilməz.
Qoldşmidtin fazalar qaydası
Qoldşmidtin fazalar qaydası - tarazlıq vəziyyətində eyni vaxtda mövcud olan mineralların sayı ilə süxuru təşkil edən sərbəst komponentlərin sayı arasında asılılıq qanunauyğunluğu. Qoldşmidtin fazalar qaydası qısa ifadəsi belədir: "İstənilən təzyiq və temperaturda n sayda komponentdən n-dən artıq mineral sabit müvazinət halında birgə mövcud ola bilməz". Qoldşmidt bu qaydanı qapalı sistemlərə aid etmişdir.
Mineral
Süxur
Təzyiq
Temperatur
Geologiya terminlərinin izahlı lüğəti. — Bakı: Nafta-Press, 2006.

Sağ əl qaydası
Sağ əl qaydası — naqildə yaranan induksiya cərayanının istiqamətini təyin edən qayda: sağ əl elə tutulur ki, maqnit sahəsinin qüvvə xətləri ovuca daxil olsun və onunla 90-li bucaq təşkil edən baş barmaq naqilin hərəkət istiqamətinə yönəlsin, bu zaman dörd barmağın vəziyyətini naqildəki induksiya cərəyanının istiqamətini göstərir.
Sol əl qaydası
Sol əl qaydası-naqildən axan cərəyan, maqnit qüvvə xətləri, və cərəyanlı naqilə təsir edən qüvvə istiqamətləri arasındakı əlaqəni müəyyənləşdirir. Bu qaydaya görə maqnit qüvvə xərləri açılmış sol əlin içərisinə daxil olduqda dörd barmaq cərəyan istiqamətində yönəlirsə açılmış baş barmaq keçiriciyə təsir edən Amper qüvvəsinin istiqamətini göstərəcək.

"Chatham House" qaydası
"Chatham House" qaydası — görüşə gələn hər kəsin müzakirədə verilən məlumatlardan istifadə etməkdə sərbəst olması, lakin həmin xüsusi şərhi kimi verdiyini açıqlamağa icazə verilmədiyi qayda. Bu, müzakirələrin daha da açıq olması üçün nəzərdə tutulmuşdur. Qayda mübahisəli mövzular üzrə debatlar və diskussiya panelləri keçirmək üçün yaradılmış bir sistemdir. Bu qayda 1927-ci ilin iyununda təsis edilmiş Kral Beynəlxalq Münasibətlər İnstitutunun Londonda yerləşən qərargahının adını daşıyır.
Qayda 1927-ci ildə yaradılmış və 1992-ci ildə təkmilləşdirilmişdir. Tərkibinə sonuncu dəfə 2002-ci ildə dəyişiklik edilmiş qaydada qeyd olunur:
Bəzi hallarda "Chatham House" qaydalarına istinad edilir. Bununla belə, "Chatham House" bildirmişdir ki, bu, bir qaydadan ibarət olduğuna görə tək halında istifadə edilməlidir.
Qayda dövlət siyasətinin və cari məsələlərin müzakirəsinin daha açıq formada aparılmasını təşviq etmək üçün nəzərdə tutulmuşdur. Bu, insanlara öz karyeraları üçün risk yaratmadan, işəgötürənlərinin rəyindən və baxışından aydın şəkildə ayrı olan mübahisəli fikirləri və arqumentləri ifadə və müzakirə etmək üçün imkan yaradır.
1927-ci ildə yaradılmış orijinal qaydaya 1992-ci ilin oktyabrında və yenidən 2002-ci ildə dəyişikliklər edilmişdir.

Texniki analiz
Texniki analiz — oxşar şəraitdə keçmişdə baş verən qiymət dəyişiklikləri nümunələri əsasında mümkün qiymət dəyişikliklərini proqnozlaşdırmaq üçün alətlər toplusu. Əsas əsas qiymət qrafiklərinin təhlili — "diaqramlar" (ing. chart — qrafik, diaqramma) və / və ya birja stəkanı. Nəzəri cəhətdən texniki analiz istənilən bazara şamil edilir. Lakin texniki analiz ən çox yüksək likvidli sərbəst bazarlarda, məsələn, birjalarda istifadə olunur.
Texniki təhlilin yaranması üçün ilkin şərtlər maliyyə bazarlarında əsrlər boyu qiymət dəyişikliklərinin müşahidəsi olmuşdur. Texniki analizin arsenalında ən qədim alət XVIII-XIX-cu əsrlərdə yapon düyü tacirləri tərəfindən hazırlanmış KEISEN metodudur (けい線). Qərbdə və Rusiyada "Yapon şamları" kimi tanınır.
XIX əsrin sonlarında amerikalı jurnalist Çarlz Dou nəzəriyyəsinin əsasını təşkil edən və XX əsrin əvvəllərində texniki analiz metodlarının sürətli inkişafının başlanğıcı kimi xidmət edən qiymətli kağızlar bazarları haqqında bir sıra məqalələr dərc etdi. XX əsrin ikinci yarısında kompüter texnologiyasının inkişafı təhlil alətlərinin və üsullarının təkmilləşdirilməsinə, həmçinin kompüter texnologiyasının imkanlarından istifadə edən yeni metodların yaranmasına kömək etdi.
Texniki bitkilər
Texniki bitkilər-məhsulu sənayedə xammal kimi istifadə olunmaq üçün becərilən bitkilərdir. texniki bitkilərə adətən əyirmə, kauçuklu, efir-yağlı, yağlı, şəkərli və dərman bitkiləri aid edilir.
Texniki xidmət
Texniki xidmət (ing. maintenance, ru.сопровождение, поддержка, эксплуатация, техническое обслуживание)-proqram təminatının istismara verilməsindən sonra təkmilləşdirilməsi, optimallaşdırılması və aşkarlanan xətaların aradan qaldırılması prosesi. Müşayiətin gedişində proqramda aşkarlanmış xətaları və çatışmazlıqları düzəltmək, eləcə də proqram təminatının istifadəsini daha əlverişli etmək məqsədilə ona yeni funksiyalar əlavə etmək üçün proqramlarda dəyişikliklər edilir. Texniki xidmət proqramları kompüterin düzgün işlənməsinə nəzarət etmək və nasazlıqları aşkar etmək üçündür. Kompüterin işinə nəzarət etmək üçün müxtəlif üsullar mövcuddur. Bu üsullardan bəziləri kompüterin aparat vasitələri ilə, bəziləri aparat proqram vasitələri ilə, bəziləri isə proqram vəsitələri həyata keçirilir. Proqramla nəzarət test proqramları və xüsusi nəzarət proqramları vasitəsilə həyata keçirilir. Testlə yoxlama kompüterin və onun ayrı-ayrı blokıarının işini yoxlayan test- proqramlar vasitəsilə yerinə yetirilir. Test proqramları adətən kompüterin daimi yaddaş qurğusunda saxlanılır və kompüter elektrik şəbəkəsinə qoşulduqda avtomatik olaraq işə düşülür. Xüsusi nəzarət proqramları kompüterdə məsələləsin həlli üçün tətbiq olunan proqramların icrası zamanı əvvəlcədən müəyyənləşdirilmiş vəziyyətlərin, asılılıqların və məhdudiyyətlərin ödənilib-ödənilməməsini yoxlayır.

Texniki dəstək
Texniki dəstək (ing. Technical support, rus. Техническая поддержка) —
Texniki dəstəyi kompüterin istehsalçısı, kompüteri aldığınız mağaza, yaxud kompüterdən "başı çıxan" tanıdığınız göstərə bilər.
İsmayıl Calallı (Sadıqov), "İnformatika terminlərinin izahlı lüğəti", 2017, "Bakı" nəşriyyatı, 996 s.

Ekoloji təhlükəsizlik
Ekoloji təhlükəsizlik—insanın və cəmiyyətin həyati vacib maraqlarının, ətraf mühitin ona antropogen və təbii təsirlər nəticəsində yarada biləcəyi təhlükələrdən qorunmasının təmin edilməsidir. Keçən əsrin sonlarında Azərbaycan müstəqilliyə qovuşduqdan sonra ekoloji təhlükəsizliyin qayğısına qaldı və bu sahəni ölkənin milli təhlükəsizlik siyasətinin əsas istiqamətlərindən biri kimi dəyərləndirdi.1999-cu ildə qəbul olunmuş "Ekoloji təhlükəsizlik haqqında" qanunun 2-ci maddəsində qanunun təsir dairəsi və məqsədi belə izah edilir: İnsan həyatını və sağlamlığını, cəmiyyət, onun maddi və mənəvi dəyərlərini, ətraf mühiti, o cümlədən, atmosfer havası, kosmik fəza, su obyektləri, yerin təki, torpaq, təbii landşaft, bitki və heyvanlar aləmini təbii və antropogen amillərin təsiri nəticəsində yaranan təhlükələrdən qorumaq üçün hüquqi əsasları müəyyən etməkdir. Ətraf mühitin mühafizəsi Azərbaycan Respublikasının dövlət siyasətinin prioritetlərindən biridir. Bu məqsədlə qəbul olunmuş dövlət proqramları ekoloji təhlükəsizliyin təmin olunması sahəsində mühüm sənəddir.
Bu məqsədlə qəbul olunmuş dövlət proqramları ekoloji təhlükəsizliyin təmin olunması sahəsində mühüm sənəddir.
— Təhlükəli ekoloji vəziyyətin yaranması və genişlənməsinə səbəb olan halları və hadisələri aşkar etmək və proqnozlaşdırmaq;
— Ekoloji təhlükəsizlikə bağlı informasiya təminatını təşkil etmək və həyata keçirmək;
— Ekoloji təhlükəsizlik sahəsində əhalinin təlimatlandırılmasını təmin etmək;
— Ekoloji təhlükəsizlikə bağlı qanunvericilikdə müəyyən edilmiş vəzifələri həyata keçirmək və s.
Ölkəmizdə ekoloji vəziyyətin ekoloji təhlükəsizlik siyasətinin istiqamətidir. Hər bir dövlət, o cümlədən, Azərbaycan ətraf mühitin mühafizəsinə xüsusi diqqət yetirir. Ekologiya ilə bağlı qəbul olunmuş qərarlar, bir sıra normativ aktlar belə deməyə əsas verir.
Azərbaycanda son illər ətraf mühitin mühafizəsi və ekoloji problemlərin həlli istiqamətində müəyyən işlər görülür.

Fiziki təhlükəsizlik
Fiziki təhlükəsizlik, obyektlərə, avadanlıqlara və mənbələrə icazəsiz girişin qarşısını almaq, işçiləri və əmlakı zərər və ziyanlardan (casusluq, oğurluq və ya terror hücumları) qorumaq üçün hazırlanmış təhlükəsizlik tədbirlərini müəyyənləşdirir. Fiziki təhlükəsizlik, qapalı dövrə televiziya nəzarəti, xüsusi təhlükəsizlik işçisi, qoruyucu baryerlər, kilidlər, giriş nəzarəti protokolları və bir çox digər texnika daxil olmaqla bir çox əlaqəli sistem təbəqəsinin istifadəsini əhatə edir.
Qorunan obyektlər üçün fiziki təhlükəsizlik sistemləri ümumiyyətlə aşağıdakıları nəzərdə tutur:
potensial müdaxilələrin qarşısını almaq (məs. xəbərdaredici nişanlar və ətraf mühit nişanları);
müdaxilə edənləri aşkar etmək və onları izləmək/qeyd etmək (məsələn, dəvətsiz qonaqların xəbərdarlığı siqnalları və CCTV sistemləri);
müvafiq hadisələrə cavabların hazırlanması (məsələn, təhlükəsizlik işçiləri və polis tərəfindən).
Kiber təhlükəsizlik
Kibertəhlükəsizlik, kompüter təhlükəsizliyi, rəqəmsal təhlükəsizlik və ya informasiya texnologiyaları təhlükəsizliyi (İT təhlükəsizliyi) — kompüter sistemləri və şəbəkələrinin məlumatlarını icazəsiz açıqlanma, texniki vasitələrin, proqram təminatının və ya verilənlərin oğurlanması, eləcə də zədələnməsi ilə nəticələ bilən zərərli aktorların hücumlarından, habelə təmin edilən xidmətlərin pozulmasından və ya yanlış istiqamətləndirilməsindən qorunmasıdır.
Bu sahə kompüter sistemləri, internet, habelə Bluetooth və Wi-Fi kimi simsiz şəbəkə standartlarına qarşı etibarın artmasına görə vacibdir. Smart telefonlar, televizorlar və əşyaların internetini (IoT) təmin edən müxtəlif cihazlar da daxil olmaqla smart cihazların artması da bu sahənin əhəmiyyətini artırır. Kibertəhlükəsizlik həm məlumat sistemlərinin qarışıq olması, həm də dəstəklədikləri cəmiyyətlərə görə müasir dünyanın ən mühüm məsələlərindən biridir. Təhlükəsizlik xüsusilə də distrubasiya, seçkilər və maliyyə kimi geniş əhatəli fiziki təsirlərə malik irimiqyaslı sistemləri idarə edən sistemlər üçün böyük əhəmiyyət daşıyır.
Kibertəhlükəsizliyin bir çox istiqaməti elektron şifrələr və şifrələmə kimi rəqəmsal müdafiə sxemlərini əhatə edir, lakin ondan həmçinin metal kilidlər kimi fiziki təhlükəsizlik müdafiələrinə yönəlmiş icazəsiz müdaxilələrin qarşısını almaq üçün hələ də istifadə edilir.
İnternetin gəlişindən və son illərdə başlanan rəqəmsal transformasiya ilə kibertəhlükəsizlik anlayışı həm peşəkar, həm də şəxsi həyatımızda tanış bir mövzuya çevrildi. Kibertəhlükəsizlik və kiber təhdidlər texnoloji dəyişikliklərin son 50 ilində ardıcıl olaraq mövcuddur. 1970 və 1980-ci illərdə kompüter təhlükəsizliyi əsasən internet konsepsiyasına qədər akademik mühitlə məhdudlaşdı, burada artan əlaqə ilə kompüter virusları və şəbəkə müdaxilələri artmağa başladı. 1990-cı illərdə virusların yayılmasından sonra 2000-ci illər kibertəhlükəsizliy və kibertəhlükəsizliyin institusionallaşdırılması aktual mövzuya çevrildi.

Milli təhlükəsizlik
Milli təhlükəsizlik — vətəndaşlar, iqtisadiyyat və digər institutlar da daxil olmaqla milli dövlətin təhlükəsizliyi. Onun təmin edilməsi hökumətin vəzifəsi hesab olunur.
Əslində hərbi hücumdan qorunma kimi qəbul edilən milli təhlükəsizlik artıq daha geniş mənalarda istifadə edilməklə qeyri-hərbi aspektləri, yəni iqtisadi təhlükəsizlik, enerji təhlükəsizliyi, ekoloji təhlükəsizlik, ərzaq təhlükəsizliyi, kiber təhlükəsizlik və s. sahələri də əhatə edir. Eynilə, milli təhlükəsizlik risklərinə digər milli dövlətlərin hərəkətləri ilə yanaşı, zorakı qeyri-dövlət subyektləri, narkokartellər və transmilli şirkətlərin fəaliyyəti, eləcə də təbii fəlakətlərin təsirləri daxildir.
Dövlətlər milli təhlükəsizliyi qorumaq üçün müxtəlif tədbirlərə, o cümlədən siyasi, iqtisadi və hərbi güc də daxil olmaqla, diplomatiyaya arxalanırlar. Hökumətlər təhlükəsizliyin transmilli səbəblərini (iqlim dəyişikliyi, iqtisadi bərabərsizlik, siyasi təcridetmə və nüvə silahlarının yayılması) azaltmaqla həm regional, həm də beynəlxalq səviyyədə təhlükəsizlik şəraiti qurmağa çalışırlar.

Təhlükəsizlik Mühəndisliyi
Təhlükəsizlik mühəndisliyi — mühəndisliyin ixtisaslaşmış sahəsi olub, informasiya sistemlərini müxtəlif mənbəli təhlükələrdən və zərərli hərəkətlərdən qorumaq üçün sistemlərin dizaynında fokuslanmışdır. Bu sahə o biri mühəndislik sahələri kimi həm istifadəçi ehtiyaclarını və funksiyalarını qarşılayır həm də əlavə olaraq sistem ehtiyatlarından suistimalı və zərərli davranışları önləyir. Bu cür məhdudiyyətlər və önləmələr security policy tərəfindən tətbiq edilir.
Neçə əsrlərdən bəri təhlükəsizlik mühəndisliyi qeyri-rəsmi təhsil sahəsi olaraq mövcud olmuşdur. Məsələn, locksmithing və security printing sahələri çox illərdir varlığını davam etdirir.
Baş verən katastrofik hadisələrə əsasən, özəlliklə 9/11 (baş verən terror aktı), Təhlükəsizlik Mühəndisliyi sürətli inkişaf edən bir sahəyə çevrilmişdir. 2006-cı ildə təqdim edilən hesabata əsasən bu sahəyə 150 milyard US$ xərclənmişdir .
Təhlükəsizlik Mühəndisliyi sosial elmlər, psixologiya, iqtisadiyat, fizika, kimya, riyaziyyat və memarlıq sahələrini müxtəlif aspektlərdən əhatə edir.
fault tree analysis kimi bəzi texnikalar təhlükəsizlik mühəndisliyindən törənmişdir.
Kriptoqrafiya kimi bəzi texnikalar öncələri hərbi tətbiqetmələr vasitəsilə məhdudlaşdırılırdı.
Təhlükəsizlik dilemması
Təhlükəsizlik Dilemması (ingiliscə: security dilemma) – beynəlxalq münasibətlərdə xüsusi termin olub, iki və ya daha çox dövlət arasında bir-birinə nəzərən daha çox təhlükəsizliyə nail olmaq məqsədilə başlayan, lakin sonda hərbi münaqişə və ya daha çox təhlükəsizliyə gətirib çıxaran rəqabəti ifadə edən paradoksa deyilir. Təhlükəsizlik dilemması beynəlxalq arenadakı anarxiyadan yaranır, çünki dövlətlər bir-birlərinin davranışlarının hansı mənaya gəldiyini — müdafiə və ya hücum meyilli olduğunu başa düşməkdə çətinlik çəkir. Anarxiya xarakterli beynəlxalq sistemdə hər bir səhvin dövlət suverenliyinin itirilməsi ilə nəticələnmə ehtimalına görə də dövlətlər digər dövlətlərə qarşı öz hərbi güclərini artırmağa çalışırlar. Məsələn, A ölkəsi öz təhlükəsizliyini artırmaq məqsədilə yeni silahlar əldə edir, lakin sistemin anarxikliyindən qaynaqlanan şəraitə görə B dövləti A dövlətinin silahları müdafiə, yoxsa hücum məqsədilə əldə etdiyini anlamaqda çətinlik çəkir və hər ehtimala qarşı B dövləti də A dövlətinin edə biləcəyi hər hansı bir hərəkətdə qorunmasız vəziyyətdə qalmamaq üçün silahlar əldə edir. B dövlətinin silahlandığını görən A dövləti də bunun özünə qarşı hazırlanmış təhlükləli addım olmasından qorxaraq daha da silahlanıb B dövlətinə qarşı gələ biləcək səviyyəyə çatmaq istəyir və beləcə qarşılıqlı silahlanma davam edir. Nəticədə hər iki dövlət ilk başda hər kəsin silahsız olduğu zamandan bəri daha təhlükəsiz şəraitlə baş başa qalırlar və bu, təhlükəsizlik dilemması adlanır. Bu termin ilk dəfə Con Herts tərəfindən 1951-ci ildə onun "Siyasi realizm və siyasi idealizm" kitabında elmi dövriyyəyə gətirilmişdir. Eyni zamanda həmin ildə britaniyalı tarixçi Herbert Batterfild özünün "Tarix və insan şəraiti" kitabında oxşar konsepsiyanı izah etmiş, lakin ona spesifik ad verməmişdir.
Təhlükəsizlik dilemması müdafiə meyilli realizmin əsas xüsusiyyətlərindən biridir. Kennet Uoltza görə vahid dünya dövləti olmadığına və sistemin anarxik olmasına görə həyatda qalmaq dövlətlərin əsas hərəkət motivasiyasıdır.
