I
сущ.
1. отношение
1) связь с чем-л., причастность, касательство к чему-л. Bu işə nisbəti var имеет отношение к этому делу, heç bir nisbəti yoxdur nəyə, kimə не имеет никакого отношения к кому, к чему
2) взаимная связь, зависимость разных величин, предметов, явлений; соотношение между чем-л. Qüvvələr nisbəti соотношение сил, мат. İki kəmiyyət arasındakı nisbət отношение между двумя величинами, ikihədli və ya binar nisbət двучленное или бинарное отношение
3) мат. частное, получаемое от деления одного числа на другое
II
послел. в отношении, по отношению к, в отношении к. Mənə nisbət в отношении меня, bizə nisbət по отношению к нам. Nəinki anasına nisbət, həm də özgələrə mehribandır он добр не только к матери, но и по отношению (в отношении) к чужим
Nisbət
Nisbət — iki ədədi müqayisə etmək üçün çıxma və bölmə əməlindən istifadə olunur. Çıxma zamanı bir ədədin o birindən neçə vahid böyük və ya kiçik olduğu tapılır. Bölmə zamanı isə bir ədədin o birindən neçə dəfə böyük və ya kiçik olduğu tapılır.
a və b ədədlərinin bölünməsindən alınan qiymətə bu ədədlərin nisbəti deyilir.Nisbətdə iştirak edən I ədədə nisbətin I həddi (əvvəlki həddi), II ədədə isə II həddi (sonrakı həddi) deyilir.
Məsələn:
I hədd:6
II hədd:3
6:3=2
Deməli 6 ilə 3-ün nisbəti 2-dir.Deməli 6 3-dən 2 dəfə böyükdür.

Nisbət Mehdiyeva
Mehdiyeva Nisbət Canməmməd qızı — tarixçi, tarix elmləri doktoru (1991), professor (1994).
Nisbət Mehdiyeva 1937-ci il yanvarın 1-də Azərbaycanda Şamaxı rayonunun Göylər kəndində anadan olmuşdur. Burada kənd məktəbini bitirdikdən sonra Azərbaycan Döviət Universitetinin tarix fakültəsində təhsil almışdır (1955—1960). Azərbaycan EA-nın Tarix İnstitutunda baş laborant, elmi işçi, ADU-da aspirant (1963—1967), Azərbaycan Dövlət Tibb İnstitutunun Sov.İKP tarixi kafedrasında müəllim və baş müəllim (1967—1973), BDU-nun SSRİ tarixi kafedrasında dosent (1973—1991), BDU-nun Türk və Qafqaz xalqları tarixi kafedrasında professor əvəzi (1991—1994) vəzifələrində olmuşdur. Hazırda kafedranın professorudur (1994-cü ildən). "Azərbaycan Həmkarlar İttifaqının partiyanın rəhbərliyi altında neft sənayesinin bərpası uğrunda mübarizəsi (1921—1925-ci illər)" mövzusunda namizədlik dissertasiyası (1968), "Azərbaycan yaradıcılıq ittifaqlarının mədəniyyətin inkişafı sahəsində fəaliyyəti (1960—1980-ci illər)" mövzusunda doktorluq dissertasiyası müdafiə etmişdir (1991). Bu, keçmiş SSRİ-də yaradıcılıq ittifaqlarının tarixinə həsr olunmuş ilk doktorluq dissertasiyasıdır. Dövri mətbuatda 50-yə yaxın elmi məqaləsi, o cümlədən dərs proqramı, elmi-metodik tövsiyələri dərc olunmuşdur. Ümumtəhsil məktəblərinin 9—10-cu sinif şagirdləri içün "Yeni tarix" kitabının şərikli müəllifı, "Türk xalqlarının tarixi (yeni dövr)" dərsliyinin müəllifidir.
Azərbaycan yaradıcılıq ittifaqlarının kütləvi təbliğat sahəsində fəaliyyəti (1960—1980-ci illər) (dərs vəsaiti).

Nisbət Sədrayeva
Nisbət Sədrayeva (17 yanvar 1998, Göylər, Şamaxı rayonu) ― azərbaycanlı muğam ifaçısı. 2010-cu ildə "Kainat" Beynəlxalq Uşaq Muğam Festivalının, 2013-cü ildə Təhsil Nazirliyinin təşkilatçılığı ilə keçirilmiş gənc ifaçıların II Respublika müsabiqəsinin, 2015-ci il V Televiziya Muğam Müsabiqəsinin və 2018-ci ildə Beynəlxalq Muğam Festivalının qalibidir. Azərbaycan Dövlət Televiziyasının və Beynəlxalq Muğam Mərkəzinin solistidir.
Nisbət Əlfəddin qızı Sədrayeva 1998-ci il 17 yanvar Şamaxı rayon Göylər kəndində anadan olub. 2004-2007-ci ildə Ə.Məmmədov adına Göylər kənd 1 saylı orta məktəbdə 4-cü sinifə qədər təhsil alıb. 2007-ci ildə ailəsi ilə birlikdə Bakı şəhərinə köçüb. Təhsilini Bakı şəhər 33 saylı Şuşa Uşaq musiqi məktəbində davam etdirib. Şuşa Uşaq musiqi məktəbində əməkdar artist Sevinc Sarıyevadan təhsil alıb. 2009-2015-ci illər də Bülbül adına Orta ixtisas musiqi məktəbində Fehruz Səxavət və xalq artisti Ağaxan Abdullayevin tələbəsi olub.
2010-cu ildə "Kainat” Beynəlxalq Uşaq Muğam Festivalında ”Heyratı” zərb muğamını ifa edərək 1-ci yerin qalibi, 2012-ci ildə SSRİ xalq artisti Bülbülün 115 illiyinə həsr olunmuş musiqi festivalında 2-ci yerin qalibi, 2013-cü ildə isə Heydər Əliyevin 90 illik yubileyinə həsr olunmuş müsabiqə də 1-ci yerə layiq görülüb.

Qızıl nisbət
Qızıl bölgü (və ya qızıl nisbət) — riyaziyyat və incəsənətdə tətbiq olunur. İki ədəd o vaxt qızıl nisbətdə olur ki, (
φ
{\displaystyle \varphi }
), onların cəminin daha böyüyünə nisbəti onlardan böyüyünün kiçiyinə nisbətinə bərabər olsun. Cəbri dildə aşağıdakı kimi yazılır:
a
+
b
a
=
a
b
≡
φ
,
{\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi ,}
burada Yunan hərfi fi (
φ
{\displaystyle \varphi }
) qızıl bölgünü bildirir və onun dəyəri:
φ
=
1
+
5
2
=
1.61803
39887
…
.
{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\ldots .}
XX əsrdən başlayaraq xeyli sənətkarlar, memarlar öz işlərini qızıl bölgüyə əsasən qurmağa çalışıblar. Xüsusən də, onlar qızıl düzbucaqlı formasında tikintilərə xüsusi yer ayırıblar. Qızıl düzbucaqlıda uzun tərəfin qısa tərəfə nisbəti qızıl bölgü əsasında qurulur.
Qızıl bölgü tarixən insanlar tərəfindən istifadə
edilməsinə baxmayaraq, ilk dəfə kim tərəfindən
kəşf edildiyi haqqında dəqiq bir məlumat yoxdur.
Euclid (e.ə. 365 – e.ə. 300), "Elementlər" adlı
nəzəriyyəsində bir xətti 1.6180339… nöqtəsindən
bölmək haqqında yazmış və bu xətti ekstrem və əhəmiyyətli nisbətdə bölmək deyə adlandırmışdı.

Nisbət və tənasüb
A ədədinin B ədədinə bölünməsindən alınan qismətə A ədədinin B ədədinə nisbəti deyilir. Yəni, nisbət, B ədədinin A ədədinin daxilində neçə dəfə yerləşdiyini əks elətdirir(A:B).
Məsələn, əgər bir səbətdə 8 ədəd naringi, digər səbətdə 6 ədəd limon varsa, onda, naringilərin sayının limonların sayına nisbətini 8:6 ( 4:3 nisbətinə ekvivalentdir) şəklində göstərəcəyik.
Bu nümunədə həmçinin, limonların sayının naringilərin sayına nisbətini 6:8 ( və ya 3:4) şəklində, naringilərin sayının bütün meyvələrin sayına nisbətini isə 8:14 (və ya 4:7) şəklində yazmaq olar.
Nisbəti təşkil edən ədədlər istənilən oxşar kəmiyyətlər ola bilər, məsələn , obyektlərin nisbəti, insanların nisbəti, düzbucaqlının eni ilə uzunluğunun nisbəti və s.
A ədədinin B ədədinə nisbətini kəsr kimi
A
B
{\displaystyle {A \over B}}
şəklində yazmaq olar. Bu kəsri istər adi, istərsə də onluq kəsr şəklində göstərmək mümkündür.
İki nisbətin bərabərliyinə Tənasüb deyilir. A ədədinin B ədədinə nisbəti (A:B) , C ədədinin D ədədinə nisbətinə (C:D) bərabərdirsə, bu tənasübü aşağıdakı kimi quracağıq:
A:B=C:D
A,B,C və D bu tənasübün hədləri adlanır. A və D tənasübün kənar hədləri, B və C isə orta hədləri adlanır.

Dörd nöqtənin mürəkkəb nisbəti
Dörd nöqtənin mürəkkəb nisbəti (ABCD) ilə işarə olunur. Proyektiv fəzanın bir düz xəttinə aid olan dörd nöqtənin mürəkkəb nisbəti üç nöqtənin sadə nisbətlərinin bölünməsindən alınan qismətə deyilir, yəni
(
A
B
C
D
)
=
[
A
B
,
C
]
[
A
B
,
D
]
{\displaystyle (ABCD)={\frac {[AB,C]}{[AB,D]}}}
Burada
[
A
B
,
C
]
{\displaystyle [AB,C]}
A
{\displaystyle A}
,
B
{\displaystyle B}
və
C
{\displaystyle C}
nöqtələrinin sadə nisbətləridir. Analoji qaydada dörd düz xəttin (şüanın) mürəkkəb nisbəti təyin olunur.
(
a
b
c
d
)
=
[
a
b
,
c
]
[
a
b
,
d
]
{\displaystyle (abcd)={\frac {[ab,c]}{[ab,d]}}}
Burada
[
a
b
,
c
]
{\displaystyle [ab,c]}
a
{\displaystyle a}
,
b
{\displaystyle b}
və
c
{\displaystyle c}
xətlərinin sadə nisbətidir.
Mürəkkəb nisbət proyektiv həndəsənin əsas anlayışlarından biridir və proyektiv çevirmənin çox mühüm variantıdır. Dörd nöqtənin mürəkkəb nisbəti proyektiv həndəsədə bir sıra teoremlərin isbatında istifadə olunur. Məsələn, Çeva və Meneley teoremləri bu nisbətin köməyi ilə isbat olunur. Dörd nöqtənin mürəkkəb nisbəti istənilən həqiqi ədədə bərabər ola bilər. Əgər dörd nöqtənin mürəkkəb nisbəti
(
−
1
)
{\displaystyle (-1)}
-ə bərabər olarsa, onda o, harmonik dördlük adlanır.
== Ədəbiyyat ==
M. Mərdanov, S. Mirzəyev, Ş. Sadıqov Məktəblinin riyaziyyatdan izahlı lüğəti.
Həndəsi nisbətlər qanunu
Həndəsi nisbətlər qanunu Bu qanun David Dalton (1803) tərəfindən kəşf olunmuşdur: Əgər iki element bir-birilə bir neçə birləşmə əmələ gətirirsə,
bunlardan birinin eyni kütləsinə düşən digər elementin kütlələri nisbəti sadə tam ədədlərin nisbəti kimidir. Məsələn, CO2 ilə CO birləşmələrində karbonla oksigenin kütlələri nisbəti 12:32 və 12:16 nisbəti kimidir. Deməli, karbonun oksigenin sabit kütləsi ilə birləşən kütlələri nisbəti 2:1-ə
nisbəti kimidir. Bu qanun əsasında Dalton hidrogenin kütləsini şərti olaraq vahid qəbul edərək elmə nisbi atom kütləsi anlayışını
daxil etmişdir. Hal-hazırda isə göstərdiyimiz kimi nisbi atom kütlə vahidi olaraq karbon-12 izotopunun molyar kütləsinin 1/12 qəbul edilmişdir.
Qiymət-mənfəət nisbəti
Qiymət-mənfəət nisbəti - şirkətin səhminin cari qiymətinin hər səhmə düşən xalis mənfəətə nisbəti. Məsələn, əgər 10 min səhmə malik şirkətin səhmi hazırda 10 manata tədavül olunursa və son ildə xalis mənfəət 5 min manata bərabərdisə, P/E nisbətini aşağıdakı qaydada tapmaq olar: Hər səhmə düşən xalis mənfəət = 10 000/5 000 = 2 P/E = 10 / 2 = 5.
Qiymət – 1)əmtəə dəyərinin pulla ifadəsi; 2)əhəmiyyət, dəyər, önəm, rol; etibar; 3)şagirdin, tələbənin bilik dərəcəsi haqqında verilən nömrə: imtahanda biliyin göstəricisi. Məsələn, orta qiymət, pis qiymət, dərslərdən əla qiymət almaq.4)hüquqda: bəzi müqavilə növlərində mühüm şərtlərdən biri; 5)iqtisadiyyatda: bir malın digər mala dəyişmə nisbəti; malların (məhsulların) və xidmətlərin dəyişmə dəyərinin pulla ifadəsi; ehtiyaclarımızı ödəmək məqsədilə mal və xidmətlərə verdiyimiz nisbi üstünlük. Məsələn, malın qiyməti; 6)pulun miqdarını göstərən fundamental iqtisadi kateqoriyadır; 7)əmtəə dəyərinin pul ifadəsi; əmtəə istehsalına sərf olunmuş ictimai zəruri iş vaxtı miqdarının dolayı ölçülməsində xidmət edən iqtisadi kateqoriya.
İntellekt nisbəti
İntellekt əmsalı (ing. intelligence quotient; abr. IQ ; təl. "ay-kü") — insanın malik olduğu intellekt qabiliyyətinin kəmiyyət göstəricisi.
Verilmiş şəxs eyni zamanda cəmiyyətdə orta statistik insanın malik olduğu intellektə nisbətən müqayisə olunur. Bunun üçün xüsusu testlər mövcuddur. IQ testləri bilik səviyyəsini yox, düşünmə qabiliyyətini aşkar etməyə xidmət edir. İntellekt əmsalı ümumi intellekt faktorunun (g) qiymətləndirilməsi üçün tətbiq edilir.
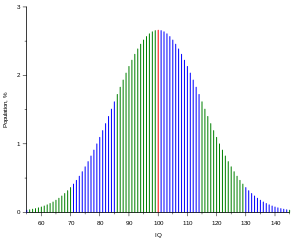
İQ testləri elə tərtib edilir ki, nəticəni mərkəzi 100%-ə bərabər İQ qiyməti olan normal səpələnmə kimi təsvir etmək mümkün olsun, belə ki, insanların 50%-i 90–110 arasında, 25%-i isə 110-dan artıq qiymətə malik olsunlar. Amerika ali məktəbinin məzununun İQ qiyməti 115, əlaçıların ki, isə 135–140 təşkil edir.

İntelekt nisbəti
İntellekt əmsalı (ing. intelligence quotient; abr. IQ ; təl. "ay-kü") — insanın malik olduğu intellekt qabiliyyətinin kəmiyyət göstəricisi.
Verilmiş şəxs eyni zamanda cəmiyyətdə orta statistik insanın malik olduğu intellektə nisbətən müqayisə olunur. Bunun üçün xüsusu testlər mövcuddur. IQ testləri bilik səviyyəsini yox, düşünmə qabiliyyətini aşkar etməyə xidmət edir. İntellekt əmsalı ümumi intellekt faktorunun (g) qiymətləndirilməsi üçün tətbiq edilir.
İQ testləri elə tərtib edilir ki, nəticəni mərkəzi 100%-ə bərabər İQ qiyməti olan normal səpələnmə kimi təsvir etmək mümkün olsun, belə ki, insanların 50%-i 90–110 arasında, 25%-i isə 110-dan artıq qiymətə malik olsunlar. Amerika ali məktəbinin məzununun İQ qiyməti 115, əlaçıların ki, isə 135–140 təşkil edir.

İnvestisiya səmərəliliyi nisbəti
İnvestisiya səmərəliliyi nisbəti (gəlirliliyin uçot dərəcəsi, investisiyanın gəlirliliyinin uçot dərəcəsi, gəlirin uçot dərəcəsi, qoyulmuş kapitalın gəlirliliyi, maliyyə hesabatı üsulu, ing. Accounting rate of return, ARR) — göstərici investisiyaların uçot gəlirliliyinə təsirini orta illik mənfəətin orta illik investisiyaya nisbəti kimi xarakterizə edir.
Kanadalı professor Entoni Atkinsonun fikrincə, mühasibat uçotu gəlirliliyi orta illik mühasibat xalis mənfəətinin orta investisiya səviyyəsinə nisbətinə bərabər qoyulmuş kapitalın gəlirlilik dərəcəsini təqribən göstərən göstəricidir.
İnvestisiya səmərəliliyi əmsalı - göstərici investisiyaların uçot gəlirliliyinə təsirini orta illik mənfəətin orta illik investisiyaya nisbəti kimi xarakterizə edir:
A
R
R
=
P
N
1
/
2
∗
(
I
+
R
I
)
{\displaystyle ARR={\frac {PN}{1/2*(I+RI)}}}
,
burada
P
N
{\displaystyle PN}
— orta illik mənfəət (nəzərdən keçən dövr üçün investisiya obyektinin orta pul vəsaitlərinin hərəkəti amortizasiya (yəni xalis mənfəət) çıxılmaqla),
I
{\displaystyle I}
- investisiya (sərmayələrin dəyəri (xərc edilmiş kapital) dövr), <math>RI< /math> — ləğvetmə dəyəri (dövrün sonunda investisiya dəyəri).
Orta illik xalis mənfəət əlavə gəlir və layihə ilə bağlı xərclər (təhlil olunan kapital qoyuluşları) arasındakı fərq kimi hesablanır.
Əgər mühasibat uçotu gəlirlilik dərəcəsi hədəf gəlir dərəcəsinin dəyərindən böyükdürsə, o zaman layihə qəbul edilir. ARR nə qədər yüksək olsa, bu layihənin cəlbediciliyi bir o qədər yüksəkdir.
ARR nisbəti pul vəsaitlərinin hərəkətinin vaxt aspektini, kapitalın qiymətini nəzərə almır və aktivlərin fəaliyyət müddətindəki fərqləri nəzərə almır. Göstərici pul vəsaitlərinin hərəkətinin məbləğini nəzərə almır, lakin xalis mənfəət əsasında hesablanır. Göstərici məlumatları ortalaşdırır və pul vəsaitlərinin hərəkətinin zamanla bölüşdürülməsi haqqında məlumat vermir, lakin bütün dövrlərdə pul vəsaitlərinin hərəkətini və məhsulun gəlirliliyini nəzərə alır.

Əvəzetmənin marjinal nisbəti
Mikroiqtisadiyyatda əvəzetmənin marjinal nisbəti — istehlakçının digər əmtəəni bir ədəd artırmaq üçün imtina etməyə hazır olduğu əmtəənin kəmiyyətini müəyyən edən kəmiyyət. Bu halda, bir məhsul digəri ilə əvəz olunur və əvəzetmənin intensivliyi sadəcə əvəzetmənin marjinal sürətini göstərir. Əvəzetmənin marjinal dərəcəsi MRS ilə işarələnir (İngiliscə marjinal əvəzetmə nisbətindən) və düsturla hesablanır:
M
R
S
x
y
=
−
(
Δ
y
/
Δ
x
)
,
{\displaystyle MRS_{xy}=-(\Delta y/\Delta x)\,,}
burada
x
{\displaystyle x}
— bir əmtəə məbləğidir,
y
{\displaystyle y}
— müvafiq olaraq başqa bir əmtəənin məbləğidir.
Δ
x
{\displaystyle \Delta x}
və
Δ
y
{\displaystyle \Delta y}
müvafiq əmtəələri dəyişdirir.
Həmçinin,
x
{\displaystyle x}
və
y
{\displaystyle y}
əmtəələrinin marjinal faydalılıqlar münasibətləri vasitəsilə (faydalılıq nəzəriyyəsinə kəmiyyət (kardinal) yanaşma ilə) marjinal əvəzetmə dərəcəsi müəyyən edilə bilər:
M
R
S
x
y
=
M
U
x
/
M
U
y
{\displaystyle MRS_{xy}=MU_{x}/MU_{y}}
Əgər fərqsizlik əyrisi anlayışına (istehlakçının laqeyd olduğu seçimdə iki əmtəənin bütün kombinasiyalarını göstərən xətt, yəni bütün bu birləşmələr ona eyni faydalılıq səviyyəsini gətirir) etibar etsək, onda marjinal əvəzetmə dərəcəsi. laqeydlik əyrisinin mailliyi kimi qəbul etmək olar. Yəni hesab edilir ki, əldə edilmiş faydalılıq səviyyəsini saxlamaq üçün istehlakçı başqa bir əmtəənin müəyyən miqdarını istehlak etməklə eyni miqdarda ümumi faydalılıq əldə etmək üçün hər hansı bir maldan imtina edə bilər. Həndəsi olaraq, MRS əks işarə ilə götürülmüş verilmiş nöqtədə laqeydlik əyrisinin tangensinin yamacının tangensinə bərabərdir.
Məsələn, istehlakçı aşağıdakı dəstlər arasında seçimə biganə yanaşır: üç alma və bir portağal - birinci dəst və iki alma və iki portağal — ikinci dəst. Bu iki nöqtədən birmənalı şəkildə laqeydlik əyrisi çəkilə bilməsə də, portağalların alma ilə əvəzlənməsinin marjinal nisbətini aşağıdakı kimi hesablamaq olar:
M
R
S
x
y
=
−
Δ
y
Δ
x
=
−
2
−
1
2
−
3
=
1
,
{\displaystyle MRS_{xy}=-{\frac {\Delta y}{\Delta x}}=-{\frac {2-1}{2-3}}=1\,,}
burada
x
{\displaystyle x}
almaların sayı,
y
{\displaystyle y}
müvafiq olaraq portağalların sayıdır,
Δ
x
{\displaystyle \Delta x}
alma istehlakının ikinci hissəsindəki dəyişiklikdir.

Ehtiyatların dövriyyəsi nisbəti
Ehtiyatların dövriyyəsi nisbəti (ing. Inventory Turnover Ratio, IT, Turnover of a Stocks, Inventory Turnover, Inventory Utilization Ratio, inventory turns, merchandise turnover, stockturn, stock turns, turns, and stock turnover) — hesabat dövründə satılmış məhsulların maya dəyərinin bu dövrdəki ehtiyatların orta məbləğinə nisbətini xarakterizə edən maliyyə göstəricisi. Bu nisbət müəyyən bir müddət ərzində şirkətin ehtiyatlarının orta hesabla neçə dəfə satıldığını göstərir. Tipik olaraq, əmsal 1 il müddətinə hesablanır. Ehtiyatlardan istifadənin səmərəliliyi onların dövriyyəsi ilə düz mütənasibdir
== Hesablama ==
Ehtiyatların dövriyyəsi əmsalı aktivlərin dövriyyəsi əmsallarına istinad edir və müəssisənin inventardan istifadə etdiyi intensivlik dərəcəsini xarakterizə edir. Zamanla ifadə edilir. Aşağıdakı kimi hesablanır:
Ehtiyatların dövriyyə nisbəti = Xalis gəlir/Satış qiymətləri ilə orta inventar
və ya
Ehtiyatların dövriyyə əmsalı = Satılan malların dəyəri/Ehtiyatların orta dəyəri.
Bu halda ehtiyatların orta həcmi aşağıdakı kimi hesablanır:
Orta inventar = Dövrün əvvəlində inventar həcmi + Dövrün sonunda inventar həcmi/2
və ya sadəcə:
Orta inventar = Son inventar.
Çoxdövrlü məlumatlar, orta aylıq göstəricilər, inventar dövriyyəsi haqqında daha dəqiq təsəvvür yaradır. Orta aylıq göstəricilərin hesablanması mövsümi dəyişiklikləri də nəzərə alır:
Orta inventar = Dövrün sonunda inventar həcmi + Ayın sonu1 + Ayın sonu2 + ...

Faizlərin ödənilməsi nisbəti
Faizlərin ödənilməsi nisbəti və ya faiz yükü (ing. Times-interest-earned ratio, ICR) — kredit üzrə faizlərin ödənilməsindən və vergilərin ödənilməsindən əvvəlki mənfəətin məbləğini faizlərin ödənilməsi xərcləri ilə müqayisə edən maliyyə göstəricisi. Şirkətlər üçün bu göstərici borclunun faiz xərclərini onun pul vəsaitlərinin hərəkəti və ya xalis mənfəəti ilə əlaqələndirən dəyərdir, dövlət üçün isə faiz ödənişlərinin ÜDM, dövlət xərcləri və ya ixrac gəlirlərinə nisbətidir.
== Ümumi məlumat və mənası ==
Bu göstərici digər borc əmsalları ilə birlikdə borclunun borc vəziyyətinin davamlılığını qiymətləndirir. Kreditor öz kredit riskini yalnız kreditin verilməsi və ya borclunun sonrakı maliyyələşdirilməsi haqqında qərar qəbul etmək üçün faiz nisbəti kimi əsas göstəriciləri müəyyən etdikdən sonra qiymətləndirə bilər. Göstəricinin komponentləri faiz ödənişi öhdəliklərindən yaranan bütün faiz xərcləridir (istisnalar: pensiya ayırmaları üzrə faizlər, bank haqları). Yüksək faiz ödəmə əmsalı aşağı kredit riski deməkdir və əksinə. Bu nisbət nə qədər yüksək olarsa, əməliyyat fəaliyyəti ilə faiz xərclərinə xidmət etmək bir o qədər asan olar. Faizlərin ödənilməsi əmsalı təkcə borc artdıqda deyil, həm də mövcud öhdəliklər üzrə faiz dərəcəsi xidmətin qeyri-mümkün olduğu səviyyəyə yüksəldikdə pisləşir.
Faiz yükü nisbətini tamamlayan əsas göstərici həm şirkətlər, həm də ayrı-ayrı ölkələr üçün müəyyən edilə bilən borc xidmətlərinin ödənilməsi nisbətidir.

Sabit nisbətlər qanunu
Sabit nisbətlər qanunu elementlər bir-birləri ilə birləşərək müəyyən birləşmələr əmələ gətirərkən onların müəyyən nisbətlərdə birləşməsinə əsaslanan qanundur. Onun tərifi bu formadadır: Bir birləşməni təşkil edən elementlərin kütlələri arasında dəyişməz bir nisbət mövcuddur. Bu qanuna isə sabit nisbətlər qanunu deyilir. Bu qanun 1799-cu ildə fransız alimi olan Cozef Prust tərəfindən kəşf edilmişdir.
Elementlərin kimyəvi cəhətdən bir yerə cəmləşdiyi zaman müəyyən bir nisbətdə birləşdiyini müəyyən etmiş Prust bu gün sabit nisbətlər qanunu olaraq bilinən qanun üçün aşağıda göstərilmiş olan tərifi vermişdir:
Bu qanuna görə məsələn, 18 qram suyun tərkibində 16 qram oksigen olarkən, qalan 2 qramda isə hidrogen vardır. 9 qram su əmələ gələrsə, onun 8 qramı oksigenin, 1 qramı isə hidrogenin payına düşür. Suyun necə alınmasından asılı olmayaraq bu nisbət tamamilə sabit qalmağa davam edir.
Bu və buna oxşayan təcrübə nəticələri ilə sabit nisbətlər qanunu qəbul edildikdən sonra Con Dalton tərəfindən 1807-ci ildə ilk elmi atom nəzəriyyəsi irəli sürülmüşdür.