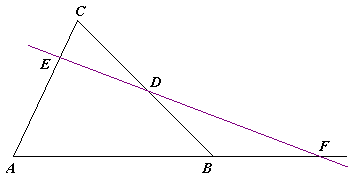
Menelay Teoremi
Menelay teoremi, transversal haqqında teorem və ya tam dördtərəfli haqqında teorem — Afin həndəsəsinin klassik teoremidir.
Bu, İskəndəriyyəli Menelaya aid edilən planimetriya teoremidir.
Əgər
A
′
,
B
′
{\displaystyle A',B'}
və
C
′
{\displaystyle C'}
nöqtələri uyğun olaraq
△
A
B
C
{\displaystyle \triangle ABC}
üçbucağının
B
C
,
C
A
{\displaystyle BC,CA}
və
A
B
{\displaystyle AB}
tərəfləri yaxud onların uzantıları üzərində olarlarsa, onda onlar yalnız və yalnız o zaman kollinear olarlar ki,
A
B
′
B
′
C
⋅
C
A
′
A
′
B
⋅
B
C
′
C
′
A
=
−
1.
{\displaystyle {\frac {AB'}{B'C}}\cdot {\frac {CA'}{A'B}}\cdot {\frac {BC'}{C'A}}=-1.}
burada
A
B
′
B
′
C
{\displaystyle {\frac {AB'}{B'C}}}
,
C
A
′
A
′
B
{\displaystyle {\frac {CA'}{A'B}}}
və
B
C
′
C
′
A
{\displaystyle {\frac {BC'}{C'A}}}
istiqamətlənmiş düz xətt parçalarının nisbətidir.