Nağd Ödəmə Əmsalı

Zəmanətli ödəmə — ilkin qiymət və sonrakı kotirovka arasında mümkün fərqi ödəmək üçün törəmə alətlər müqaviləsi üzrə ödəmə. Zəmanət haqqı anlayışı müştəri tərəfindən ilkin olaraq ödənilən sifariş üçün ümumi ödəniş məbləğinin onun icrası zamanı sifarişdən mümkün imtinanın qarşısını almaq üçün nəzərdə tutulmuş hissəsinə aiddir. Sifarişdən imtina zəmanət haqqının itirilməsi ilə nəticələnir. Münasibətlərdə qeydə alınan ən çox rast gəlinən hal kirayəçinin kirayə üçün təhlükəsizlik depozitinin köçürülməsidir. Bu təcrübə geniş yayılmışdır və təhlükəsizlik depozitləri demək olar ki, bütün annuitet müqavilələrində görünür. Üstəlik, söhbət təkcə daşınmaz əmlakdan deyil, həm də avadanlıqların, avtomobillərin və digər məişət əşyalarının icarəsindən gedir. Ancaq belə bir geniş yayılmış fenomen heç bir şəkildə qanunvericinin diqqətinə təsir etmədi — burada birbaşa və aydın tənzimləmə yoxdur. Buna görə də, mühasibat uçotu apararkən, mümkün olduqda onları vəziyyətə "tənzimləmək" üçün standart normaları tətbiq etmək lazımdır. İcarəyə götürən tərəfindən kirayə müqaviləsinin rəsmi imzalanmasından əvvəl də köçürülən təminat depozitinin əsas məqsədi onun belə bir müqavilə bağlamaq niyyətini maddi cəhətdən təsdiqləməkdir. Bu o deməkdir ki, əmanət qoymağın bütün əlamətləri mövcuddur.

Müstəvi üzərində (x1,y1) və (x2,y2) koordinatlarında iki nöqtə verildikdə, bu nöqtələrdən keçən düz xəttin bucaq əmsalı m, m = y 2 − y 1 x 2 − x 1 {\displaystyle m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}} düsturu ilə tapılır.

Jakkard əmsalı (Jaccard’s coefficient) və ya Jakkard ölçüsü – mətnlərin orijinallığının yoxlanılması texnologiyalarında istifadə edilən ölçüdür. Jakkard əmsalından mətnlərin orijinallığının yoxlanılmasına həsr edilmiş elmi-tədqiqat işlərində geniş istifadə edilir. Jakkard oxşarlıq formulu – mətnlərin orijinallığının yoxlanılması texnologiyalarında istifadə edilən düstur. Bu düstura görə müqayisə edilən sətirlər tamamilə üst-üstə düşürsə onda onun qiyməti 1-ə bərabərdir. Lakin bu düstur müqayisə edilən mətnlərin ölçülərində fərqləri, istifadə tezliyini və s. nəzərə almır. == Ədəbiyyat == Əliquliyev R. M., Ağayev N. B., Alıquliyev R. M., Plagiatlıqla mübarizə texnologiyaları // Bakı. İnformasiya Texnologiyaları nəşriyyatı. 2015.

Lerner əmsalı, və ya Lerner indeksi, sənaye bazarı nəzəriyyəsi sahəsində — qiymətin marjinal xərcdən nisbi artıqlığına bərabər olan firmanın bazar gücünün ölçüsü. Əmsal 1934-cü ildə iqtisadçı Abba Lerner tərəfindən təklif edilmişdir. Əmsal qeyri-kamil rəqabət şəraitində bazar gücünü qiymətləndirmək üçün istifadə edilə bilər. Məsələn, monopoliyalar. == Tərifi == Bazar gücünün göstəricisi satış qiymətinin marjinal dəyəri üstələyən məbləğin qiymətindəki payıdır. Bu dəyər ticarət əlavəsi adlanır (ing. mark-up). L = P − M C P {\displaystyle L={\frac {P-MC}{P}}} burada P {\displaystyle P} — məhsulun qiyməti; M C {\displaystyle MC} — marjinal dəyəri. Əmsal sıfırdan birə qədər olan dəyərləri qəbul edir. Nə qədər böyükdürsə, firmanın sövdələşmə gücü bir o qədər yüksəkdir.

Sortino əmsalı — investisiya alətinin, portfelinin və ya strategiyasının gəlirliliyini və riskini qiymətləndirməyə imkan verən göstərici. Sortino nisbəti Sharpe nisbətinə bənzər şəkildə hesablanır, lakin portfel dəyişkənliyi əvəzinə "aşağı dəyişkənlik" istifadə olunur. Bu halda volatillik minimum portfel gəlirindən (MAR) aşağı olan gəlirlərdən hesablanır. S = R − T σ {\displaystyle S={\frac {R-T}{\sigma }}} , burada: R {\displaystyle R} — orta portfel gəliri, T {\displaystyle T} — minimum icazə verilən portfel gəliri, σ {\displaystyle {\sigma }} — "dəyişkənlik azaldı": σ = ∫ − ∞ T ( T − x ) 2 f ( x ) d x {\displaystyle {\sigma }={\sqrt {\int _{-\infty }^{T}(T-x)^{2}\,f(x)\,dx}}} . Aşağıda qeyd olunan səbəblərə görə, davamlı düstur bir sıra gəlirlərdən götürülmüş hədəf dəyərdən aşağı dövri gəlirlərin standart kənarlaşmasını təyin edən daha sadə diskret versiyaya üstünlük verilir. Davamlı forma, bütün sonrakı hesablamaları illik gəlirlərdən istifadə etməklə aparmağa imkan verir ki, bu da investorların investisiya məqsədlərini bildirməsinin təbii yoludur. Diskret forma aylıq gəlirləri tələb edir ki, mənalı hesablamalar aparmaq üçün kifayət qədər məlumat nöqtəsi olsun ki, bu da öz növbəsində illik hədəfin aylıq hədəfə çevrilməsini tələb edir. Bu, müəyyən edilmiş riskin miqyasına əhəmiyyətli dərəcədə təsir göstərir. Məsələn, bir il ərzində hər ay 1% qazanmaq məqsədi, illik 12% qazanmaq kimi görünən ekvivalent hədəfdən daha çox risklə nəticələnir. Davamlı formanın diskret formaya üstünlük verməsinin ikinci səbəbi Sortino və Forsey (1996) tərəfindən təklif edilmişdir: “İnvestisiya etməzdən əvvəl biz nəticənin nə olacağını bilmirik...

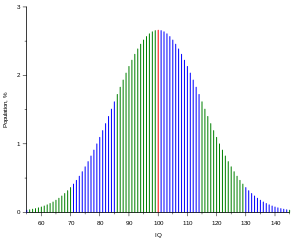
İntellekt əmsalı (ing. intelligence quotient; abr. IQ ; təl. "ay-kü") — insanın malik olduğu intellekt qabiliyyətinin kəmiyyət göstəricisi. Verilmiş şəxs eyni zamanda cəmiyyətdə orta statistik insanın malik olduğu intellektə nisbətən müqayisə olunur. Bunun üçün xüsusu testlər mövcuddur. IQ testləri bilik səviyyəsini yox, düşünmə qabiliyyətini aşkar etməyə xidmət edir. İntellekt əmsalı ümumi intellekt faktorunun (g) qiymətləndirilməsi üçün tətbiq edilir. İQ testləri elə tərtib edilir ki, nəticəni mərkəzi 100%-ə bərabər İQ qiyməti olan normal səpələnmə kimi təsvir etmək mümkün olsun, belə ki, insanların 50%-i 90–110 arasında, 25%-i isə 110-dan artıq qiymətə malik olsunlar. Amerika ali məktəbinin məzununun İQ qiyməti 115, əlaçıların ki, isə 135–140 təşkil edir.

Şarp əmsalı — orta risk mükafatının portfelin orta kənarlaşmasına nisbəti kimi hesablanan investisiya portfelinin (aktivinin) səmərəliliyinin göstəricisi. S = E [ R − R f ] σ = E [ R − R f ] V a r [ R − R f ] {\displaystyle S={\frac {E[R-R_{f}]}{\sigma }}={\frac {E[R-R_{f}]}{\sqrt {Var[R-R_{f}]}}}} , burada R {\displaystyle R} — portfel (aktiv) gəliri R f {\displaystyle R_{f}} — alternativ investisiya gəliri (adətən risksiz faiz dərəcəsi kimi qəbul edilir) E [ R − R f ] {\displaystyle E[R-R_{f}]} — risk mükafatı (riyazi gözlənti aktivlər üzrə gəlirin alternativ investisiya gəlirindən artıqlığı) σ {\displaystyle \sigma } — standart sapma portfel (aktiv) gəliri Əgər R f {\displaystyle R_{f}} sözügedən dövr ərzində sabitdirsə, o zaman V a r [ R − R f ] = V a r [ R ] {\displaystyle {\sqrt {Var[R-R_{f}]}}={\sqrt {Var[R]}}} . Şarp nisbəti aktivin gəlirinin investorun götürdüyü riski nə qədər kompensasiya etdiyini müəyyən etmək üçün istifadə olunur. Eyni gözlənilən gəlirli iki aktivi müqayisə edərkən, Sharpe nisbəti daha yüksək olan aktivə investisiya etmək daha az riskli olacaq. Şarp əmsalı gəlirlərinin illik faizlə ifadə edilən orta aylıq gəlirlərə (yaxud başqa vaxt ərzində gəlirlərə) əsaslanaraq ölçülməsi il ərzində performansı qiymətləndirməkdənsə, növbəti ayda mümkün performansı qiymətləndirmək üçün daha uyğundur. Sharpe nisbətində istifadə olunan gəlir ölçüsü uzun müddət ərzində potensial gəlirləri qiymətləndirərkən çox yanıltıcı ola bilər. Şarp nisbəti (yalnız məhdud "dəyişkənliyi aşağı" hesab edən Sortino nisbətindən fərqli olaraq) aktiv dəyərlərində yuxarı və aşağı dalğalanmalar arasında fərq qoymur. O, riski yox, portfelin məcmu dəyişkənliyini ölçür. Şarp nisbəti yuvarlanan və ardıcıl itkilər arasında fərq qoymur William F. Sharpe. The Sharpe ratio Джек Швагер.

İntellekt əmsalı (ing. intelligence quotient; abr. IQ ; təl. "ay-kü") — insanın malik olduğu intellekt qabiliyyətinin kəmiyyət göstəricisi. Verilmiş şəxs eyni zamanda cəmiyyətdə orta statistik insanın malik olduğu intellektə nisbətən müqayisə olunur. Bunun üçün xüsusu testlər mövcuddur. IQ testləri bilik səviyyəsini yox, düşünmə qabiliyyətini aşkar etməyə xidmət edir. İntellekt əmsalı ümumi intellekt faktorunun (g) qiymətləndirilməsi üçün tətbiq edilir. İQ testləri elə tərtib edilir ki, nəticəni mərkəzi 100%-ə bərabər İQ qiyməti olan normal səpələnmə kimi təsvir etmək mümkün olsun, belə ki, insanların 50%-i 90–110 arasında, 25%-i isə 110-dan artıq qiymətə malik olsunlar. Amerika ali məktəbinin məzununun İQ qiyməti 115, əlaçıların ki, isə 135–140 təşkil edir.

Borc əmsalı (ing. debt ratio) — şirkətin borc vəsaitləri ilə təmin edilmiş aktivlərinin nisbəti. == Hesablama == Borc nisbəti şirkətin ümumi öhdəliklərinin onun ümumi aktivlərinə nisbəti kimi hesablanır (şirkətin imici daxil olmaqla, şirkətin cari və əsas vəsaitlərinin cəmi). Borc nisbəti = Ümumi öhdəliklər Ümumi aktivlər {\displaystyle {\mbox{Borc nisbəti}}={\frac {\mbox{Ümumi öhdəliklər}}{\mbox{Ümumi aktivlər}}}} Məsələn, 2 milyon dollar aktivi və 500.000 dollarlıq öhdəlikləri olan bir şirkətin borc nisbəti 25% olacaq. == Göstərici dəyəri == Bu nisbət şirkətin aktivlərinin borc vəsaitləri hesabına maliyyələşdirilən hissəsinin olduğunu göstərir. 0,5 və ya daha az nisbət şirkətin ilk növbədə özünü maliyyələşdirdiyini göstərir. Ümumi aktiv strukturunda borc vəsaitlərinin payı yüksək olan şirkətin yüksək levirici olduğu deyilir. Bu göstərici nə qədər yüksəkdirsə, şirkətin gələcək fəaliyyəti ilə bağlı risk bir o qədər yüksəkdir. Bundan əlavə, yüksək göstərici dəyəri həm də şirkətin borc əldə etmək qabiliyyətinin zəif olduğunu göstərə bilər ki, bu da şirkətin maliyyə çevikliyini poza bilər (zəruri vaxtlarda lazımi vəsait toplamaq imkanı). Digər maliyyə əmsalları kimi, şirkətin borc əmsalı həmişə onun sənaye ortalaması və ya rəqiblərinin orta göstəricisi ilə müqayisə edilməlidir.

Effektivlik əmsalı (Return on Investment, ROI) — investisiyanın gəlirliliyini və kapitaldan istifadənin səmərəliliyini qiymətləndirmək üçün istifadə olunan maliyyə göstəricisidir. ROI faizlə ifadə edilir və investisiyanın gəliri ilə layihə və ya aktivə yatırılan məbləğ arasında əlaqəni ölçür. ROI hesablamaq üçün formula aşağıdakı kimidir: ROI = (Mənfəət — İnvestisiya) / İnvestisiya * 100 Mənfəətə investisiyadan əldə edilən gəlir, əlavə olaraq hər hansı əlavə fayda və ya qənaət daxildir. İnvestisiya bir layihəyə qoyulan pul məbləğini və ya aktivlərin dəyərini əks etdirir. Performans nisbəti investorlara və sahibkarlara investisiyalarının gəlirliliyini qiymətləndirməyə və onu digər investisiya imkanları ilə müqayisə etməyə imkan verir. O, həmçinin investisiya portfelinin optimallaşdırılması və ya konkret layihənin fəaliyyətinin təhlili ilə bağlı qərarlar qəbul etmək üçün istifadə edilə bilər. Qeyd etmək lazımdır ki, ROI investisiyanın qiymətləndirilməsi üçün yeganə metrik deyil. Xalis indiki dəyər (NPV), daxili gəlir dərəcəsi (IRR) və s. kimi digər göstəricilər də investisiyanın gəlirliliyini və riskini tam təhlil etmək üçün istifadə edilə bilər. Səmərəlilik nisbəti maliyyə analitikası, layihənin idarə edilməsi, sahibkarlıq və şəxsi maliyyə planlaşdırması da daxil olmaqla müxtəlif sahələrə tətbiq oluna bilər.

Geri ödəmə müddəti metodu (ing. payback period) — ilə bir investisiyaya çəkilən xərcin nə qədər müddətə geri dönəcəyi hesablanır.[1] Misal üçün hər il 1000 AZN gəlir gətirən 3000 AZN-lik bir investisiya üç illik geri ödəmə müddətinə sahibdir. İnvestisiyanın gətirdiyi gəlirlərin kumulyativ cəminin investisiya məbləğinə bərabər olduğu və ya onu keçdiyi il geri ödəmə ili olur. == Məqsədi == Geri ödəmə müddəti metodu tez-tez istifadə edilən bir metoddur. Çünki akademik təhsil və çalışma sahəsindən asılı olmayan çox insan üçün istifadəsi asan və anlaşıqlıdır. Müəssisə bu metod vasitəsilə investisiya xərclərinin nə zaman geri dönəcəyini görür və buna uyğun olaraq investisiya layihəsinin reallaşdırılması ilə bağlı qərarını verir. == Düsturu == Geri ödəmə müddəti əsasən il olaraq ifadə olunur. Hər il üçün xalis nağd pul mədaxili(1) = Nağd pul mədaxili(1) — nağd pul məxarici(1)hesablanır. Daha sonra xalis nağd pul mədaxillərinin kumulyativ cəmi hesablanır. Cəmi investisiya məbləğinə bərabər edən il isə geri ödəmə ili olur.[2] Əgər hər il üçün pul daxil olmaları sabit(eyni) olarsa, geri ödəmə müddəti = İnvestisiya məbləği(C0) / təxmin olunan xalis nağd pul mədaxili(C) P P = C 0 C {\displaystyle PP={\mathbb {C} _{0} \over C}} Pul daxil olmaları müxtəlif olduqda isə aşağıdakı düsturdar istifadə edilir: P P = n + ( C 0 − C k ) C {\displaystyle {\displaystyle PP={n+{{(\mathbb {C} _{0}-\mathbb {C} _{k})} \over C}}}} [3] n — Pul daxilolmaların kumulyativ cəminin müsbətə keçdiyi ildən əvvəlki il C0 — İnvestisiya məbləği Ck — n -ci ilə qədər(n-ci ildə daxil olmaqla) pul daxil olmalarının kumulyativ cəmi Bu düstur geri ödəmə müddətindən sonra ortaya çıxacaq dəyərləri (mənfi və ya müsbət) nəzərə almır.

Nağd pul axını qabarıqlığı — müddətinin faiz dərəcələrinə həssaslığının ölçüsü olan bir alətin (məsələn, istiqrazlar) pul axınının bir xüsusiyyəti. Dolğunluq faiz dərəcələrinin istiqrazın pul axınının cari dəyərinə təsirini aydınlaşdırmaq üçün ikinci sifariş düzəlişidir. Dəyişiklik, mövcud dəyərin faiz dərəcəsindən asılılığının qeyri-xətti olması ilə əlaqədardır, bu səbəbdən bu asılılığın müddətdən istifadə edərək xətti ilə müəyyənləşdirilməsi faiz dərəcələrinin təsirini dəqiq əks etdirə bilməz. Konveksliyin nəzərə alınması, faiz dərəcələrinin artırılması və azalması zamanı dərəcələrin təsirinin asimmetriyasını nəzərə almaq da daxil olmaqla faiz dərəcələrinin təsirini aydınlaşdırmağa imkan verir. Ümumiyyətlə, qabarıqlıq nə qədər yüksək olarsa, istiqraz qiyməti faiz nisbətinə o qədər həssas olur və istiqraz qiyməti faiz nisbətinə o qədər həssas olur. Hazırkı dəyər funksiyasının Teylor sırasındakı ilk iki termini istifadə edərək faiz dərəcəsinə qarşı P V ( r ) {\displaystyle PV(r)} əldə edirik: Δ P V ( r ) ≈ P V ′ ( r ) Δ r + 0.5 P V ″ ( r ) [ Δ r ] 2 {\displaystyle \Delta PV(r)\approx PV'(r)\Delta r+0.5PV''(r)[\Delta r]^{2}} Bu ifadəni PV (r) ilə bölsək əldə edirik: δ P V = Δ P V P V ≈ P V ′ P V Δ r + 0.5 P V ″ P V [ Δ r ] 2 {\displaystyle \delta PV={\frac {\Delta PV}{PV}}\approx {\frac {PV'}{PV}}\Delta r+0.5{\frac {PV''}{PV}}[\Delta r]^{2}} Birinci amil, durasiya işarəsi ilə müddətdir ( r {\displaystyle r} nizamlı bir nisbətdirsə, logaritmik deyilsə dəyişdirilir), ikincisi isə istədiyiniz qabarıqlıqdır (eyni vəziyyətdə dəyişdirilmişdir). M C = P V ″ ( r ) P V = ∑ i C F i ( 1 + r ) t i + 2 t i ( t i + 1 ) P V = ∑ i C F i ( 1 + r ) t i t i ( t i + 1 ) P V ( 1 + r ) 2 = T ( T + 1 ) ¯ / ( 1 + r ) 2 = ( T 2 ¯ + T ¯ ) / ( 1 + r ) 2 {\displaystyle MC={\frac {PV''(r)}{PV}}={\frac {\sum _{i}{\frac {CF_{i}}{(1+r)^{t_{i}+2}}}t_{i}(t_{i}+1)}{PV}}={\frac {\sum _{i}{\frac {CF_{i}}{(1+r)^{t_{i}}}}t_{i}(t_{i}+1)}{PV(1+r)^{2}}}={\overline {T(T+1)}}/(1+r)^{2}=({\overline {T^{2}}}+{\overline {T}})/(1+r)^{2}} C = o v e r l i n e T 2 + o v e r l i n e T {\displaystyle C=\ overline{T^{2}}+\ overline{T}} ifadəsi ümumiyyətlə "qabarıqlıq" adlanır. Həqiqi dəyər M C {\displaystyle MC} "dəyişdirilmiş qabarıqlıq" dır. Bir ilk təxmini olaraq, qabarıqlıq olaraq D ( D + 1 ) {\displaystyle D(D+1)} dəyərini də istifadə edə bilərsiniz, burada D = o v e r l i n e T {\displaystyle D=\ overline{T}} - durasiya , lakin hesablamaların dəqiqliyini azaldır. MC-nin dəyişdirilmiş müddətlə aşağıdakı şəkildə əlaqəli olduğunu göstərmək olar: M C = M D 2 − d M D d r {\displaystyle MC=MD^{2}-{\frac {dMD}{dr}}} Qiymət dəyişikliyinin ən dəqiq qiymətləndirməsi bir Taylor seriyasına cari dəyərin özü deyil, logaritması və yalnız faiz dərəcəsi ilə deyil, loqaritmik nisbətdə ln ⁡ ( 1 + r ) {\displaystyle \ln(1+r)} genişlənərək əldə edilir.

Aktivlərin dövriyyəsi əmsalı (ing. assets turnover ratio) — aktivlərdən istifadənin səmərəliliyini əks etdirən maliyyə göstəricisi. Şirkətin öz aktivlərini nə dərəcədə effektiv idarə etdiyini, cari və ya proqnozlaşdırılan satış həcmləri ilə əlaqədar şirkətin balansındakı aktivlərin ümumi sayının kifayət qədər, böyük və ya kiçik olub olmadığını təhlil etmək üçün istifadə olunur. Aktivlərə həddən artıq sərmayə qoyuluşu sərbəst pul axınını və şirkətin səhm qiymətini azaldır. Aktivlərə az investisiya qoyulması adətən satış həcminin azalması ilə nəticələnir ki, bu da sərbəst pul axını və səhm qiymətlərini azaldır. == Tərifi == iqtisadiyyatda iki məna var: məhsul satışından əldə edilən gəlir aktivlərin orta illik dəyərinə nisbəti. Bu nisbət satış həcmi baxımından aktivlərdən istifadənin səmərəliliyini xarakterizə edir. Təhlil edilən dövr üçün bir rubl aktivlərin dövriyyələrinin sayını göstərir. Formula: K = Məhsulların satışından əldə edilən gəlir / Aktivlərin orta illik dəyəri qarşılıqlı investisiya fondu ticarət fəaliyyətinin göstəricisi. Portfelinin tərkibinin nə qədər tez-tez dəyişdiyini nümayiş etdirir.

Kapitalın adekvatlıq əmsalı (ing. capital adequacy ratio, CAR) — borcalanın müflisləşməsi zamanı maliyyə itkilərini öz vəsaitləri hesabına ödəmək qabiliyyətini əks etdirən bank sabitliyinin göstəricisi. Göstərici bankın kapitalının onun riskinə nisbətinə bərabərdir. Bank tənzimləyiciləri bankların məqbul səviyyədə itkiləri bərpa edə bilmələrini və müəyyən edilmiş kapital tələblərinə əməl etmələrini təmin etmək üçün bankların bu göstəricisinə nəzarət edirlər. Bu əmsal risklə ölçülən kreditlərin həcminin faizi kimi ifadə edilir. Bu nisbətin tələb olunan səviyyəsini saxlamaq öhdəliyi əmanətçiləri qorumaq və bütün dünyada maliyyə sistemlərinin sabitliyini və səmərəliliyini təşviq etmək məqsədi daşıyır. == Hesablanması == Kapital adekvatlığı əmsalı (CAR) bankın əsas kapitalının (ing. core capital) bankın risklə ölçülmüş aktivlərinə bölünməsi faizidir: CAR {\displaystyle {\mbox{CAR}}} = 1-ci dərəcəli kapital + 2-ci dərəcəli kapital/Risklə ölçülmüş aktivlər burada: 1-ci dərəcəli kapital ( T 1 {\displaystyle T_{1}} ) = (ödənilmiş nizamnamə kapitalı + məcburi ehtiyatlar + açıqlanmış sərbəst ehtiyatlar) - (törəmə müəssisənin kapitalına investisiya + qeyri-maddi aktivlər + cari zərərlər və onların köçürülmüş qalıqları) , 2-ci dərəcəli kapital ( T 2 {\displaystyle T_{2}} ) = A) Açıqlanmamış ehtiyatlar + B) Ümumi zərər ehtiyatları + C) Hibrid borc alətləri və subordinasiya edilmiş borc alətləri, Risk ya bankın risklə ölçülmüş aktivləri ( a {\displaystyle \,a} ) və ya müvafiq ölkənin milli bank tənzimləyicisi tərəfindən müəyyən edilmiş minimum məcmu kapital tələbi ola bilər. Risk ölçülmüş aktivlərdən istifadə edərkən, CAR = T 1 + T 2 a {\displaystyle {\mbox{CAR}}={\cfrac {T_{1}+T_{2}}{a}}} ≥ 10 %. Minimum həddi (faizlə) bankdan banka dəyişir (bu halda 10%, bank tənzimləyicisinin Bazel sazişlərinin normalarına uyğun adi tələbi; ayrı-ayrı ölkələrin milli bank tənzimləyicisi tərəfindən müstəqil olaraq müəyyən edilir).