tümsek
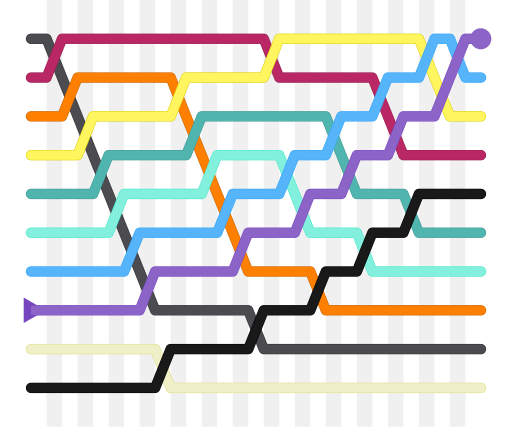
Qabarcıq nizamlama
Qabarcıqlı nizamlama və ya qabarcıqlı sıralama (ing. Bubble sort) — iki qonşu elementi müqayisə etməklə və əgər onlar səhv nizamda isə onların yerini dəyişməklə verilən siyahını təkrarla yoxlayaraq, sıralayan alqoritmdir. Alqoritmin performansı aşağıdakı kimidir:
ən yaxşı vaxt =
O
(
n
)
{\displaystyle O(n)}
orta vaxt =
O
(
n
2
)
{\displaystyle O(n^{2})}
"5 1 4 2 8" şəklində bir massiv götürək, və massivi artma sırasına görə sıralayaq. Hər bir addımda müqayisə olunan elementlər tünd qara ilə göstərilib.
Sona qədər sıralama üçün 3 keçid lazımdır.
Birinci keçid:
( 5 1 4 2 8 )
→
{\displaystyle \to }
( 1 5 4 2 8 ), Burada alqoritm ilk iki elementi müqayisə edir və 5>1 olduğu üçün 5 ilə 1-in yerini dəyişir.
( 1 5 4 2 8 )
→
{\displaystyle \to }
( 1 4 5 2 8 ), 5 > 4 olduğu üçün
( 1 4 5 2 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 > 2 olduğu
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 < 8, heç bir dəyişiklik olmur.
İkinci keçid:
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 )
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 ), 4 > 2 olduğu üçün
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Hal - hazırda massiv artma sırasına görə sıralanıb (nizamlanıb). Amma alqoritm bunun belə olduğunu bilmədiyi üçün elementlərin yerini dəyişmədən birdaha elementləri müqayisə edəcək.
Üçüncü keçid:
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Python dilində implementasiya aşağıdakı kimi olar.
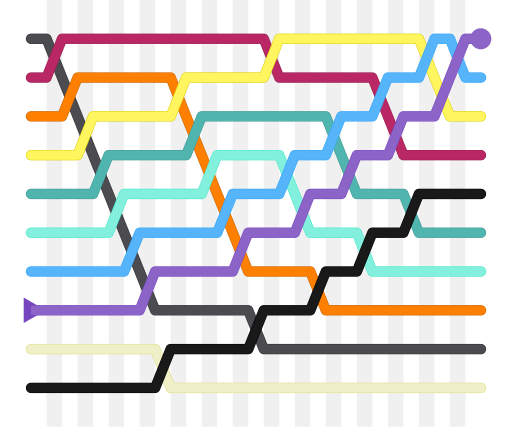
Qabarcıq sıralama
Qabarcıqlı nizamlama və ya qabarcıqlı sıralama (ing. Bubble sort) — iki qonşu elementi müqayisə etməklə və əgər onlar səhv nizamda isə onların yerini dəyişməklə verilən siyahını təkrarla yoxlayaraq, sıralayan alqoritmdir. Alqoritmin performansı aşağıdakı kimidir:
ən yaxşı vaxt =
O
(
n
)
{\displaystyle O(n)}
orta vaxt =
O
(
n
2
)
{\displaystyle O(n^{2})}
"5 1 4 2 8" şəklində bir massiv götürək, və massivi artma sırasına görə sıralayaq. Hər bir addımda müqayisə olunan elementlər tünd qara ilə göstərilib.
Sona qədər sıralama üçün 3 keçid lazımdır.
Birinci keçid:
( 5 1 4 2 8 )
→
{\displaystyle \to }
( 1 5 4 2 8 ), Burada alqoritm ilk iki elementi müqayisə edir və 5>1 olduğu üçün 5 ilə 1-in yerini dəyişir.
( 1 5 4 2 8 )
→
{\displaystyle \to }
( 1 4 5 2 8 ), 5 > 4 olduğu üçün
( 1 4 5 2 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 > 2 olduğu
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 < 8, heç bir dəyişiklik olmur.
İkinci keçid:
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 )
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 ), 4 > 2 olduğu üçün
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Hal - hazırda massiv artma sırasına görə sıralanıb (nizamlanıb). Amma alqoritm bunun belə olduğunu bilmədiyi üçün elementlərin yerini dəyişmədən birdaha elementləri müqayisə edəcək.
Üçüncü keçid:
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Python dilində implementasiya aşağıdakı kimi olar.
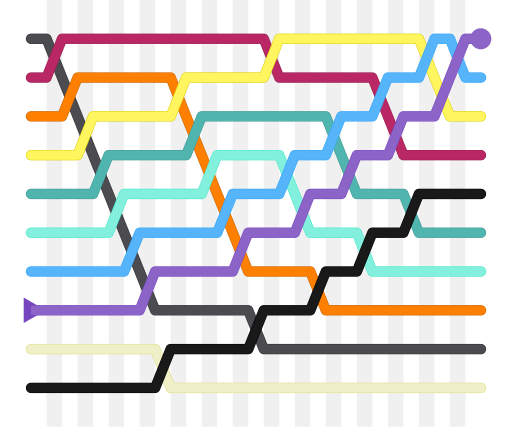
Qabarcıqlı nizamlama
Qabarcıqlı nizamlama və ya qabarcıqlı sıralama (ing. Bubble sort) — iki qonşu elementi müqayisə etməklə və əgər onlar səhv nizamda isə onların yerini dəyişməklə verilən siyahını təkrarla yoxlayaraq, sıralayan alqoritmdir. Alqoritmin performansı aşağıdakı kimidir:
ən yaxşı vaxt =
O
(
n
)
{\displaystyle O(n)}
orta vaxt =
O
(
n
2
)
{\displaystyle O(n^{2})}
"5 1 4 2 8" şəklində bir massiv götürək, və massivi artma sırasına görə sıralayaq. Hər bir addımda müqayisə olunan elementlər tünd qara ilə göstərilib.
Sona qədər sıralama üçün 3 keçid lazımdır.
Birinci keçid:
( 5 1 4 2 8 )
→
{\displaystyle \to }
( 1 5 4 2 8 ), Burada alqoritm ilk iki elementi müqayisə edir və 5>1 olduğu üçün 5 ilə 1-in yerini dəyişir.
( 1 5 4 2 8 )
→
{\displaystyle \to }
( 1 4 5 2 8 ), 5 > 4 olduğu üçün
( 1 4 5 2 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 > 2 olduğu
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 < 8, heç bir dəyişiklik olmur.
İkinci keçid:
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 )
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 ), 4 > 2 olduğu üçün
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Hal - hazırda massiv artma sırasına görə sıralanıb (nizamlanıb). Amma alqoritm bunun belə olduğunu bilmədiyi üçün elementlərin yerini dəyişmədən birdaha elementləri müqayisə edəcək.
Üçüncü keçid:
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Python dilində implementasiya aşağıdakı kimi olar.

Qabarcıqlı yaddaş
==Qabarcıqlı yaddaş==
Qabarcıqlı yaddaş– silindrik maqnit domenlərdən (nazik pərdə üzərində yerləşdirilmiş halqaşəkilli sabit maqnitlərdən) təşkil olunmuş yaddaş tipi. Qabarcıqlı yaddaşa nisbətən az rast gəlinir; operativ yaddaşdan (RAM) və daimi yaddaşdan (ROM) bahadır. Qabarcıqlı yaddaşın üstünlüyü onun sabitliyindədir (daimiliyindədir): ona yazılmış hər hansı bir şey hətta kompüter söndürüldükdə də dəyişdirilməyənə qədər saxlanılır. Fləş-yaddaşlar meydana çıxandan sonra qabarcıqlı yaddaşlara olan tələbat praktik olaraq azalıb, çünki fləş-yaddaşlar da daimi saxlama xassəsinə malikdir və həm də onların hazırlanması asan və ucuz başa gəlir.
İsmayıl Calallı (Sadıqov), “İnformatika terminlərinin izahlı lüğəti”, 2017, “Bakı” nəşriyyatı, 996 s.
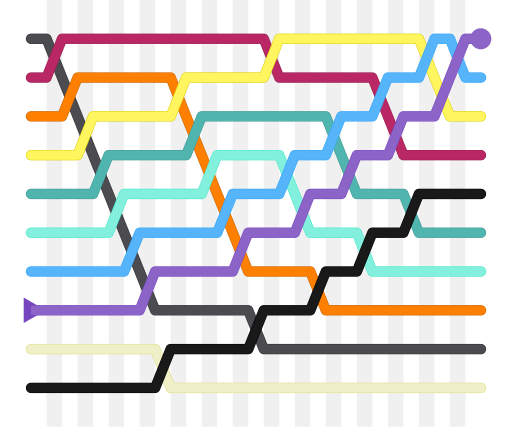
Qabarcıqlı çeşidləmə
Qabarcıqlı nizamlama və ya qabarcıqlı sıralama (ing. Bubble sort) — iki qonşu elementi müqayisə etməklə və əgər onlar səhv nizamda isə onların yerini dəyişməklə verilən siyahını təkrarla yoxlayaraq, sıralayan alqoritmdir. Alqoritmin performansı aşağıdakı kimidir:
ən yaxşı vaxt =
O
(
n
)
{\displaystyle O(n)}
orta vaxt =
O
(
n
2
)
{\displaystyle O(n^{2})}
"5 1 4 2 8" şəklində bir massiv götürək, və massivi artma sırasına görə sıralayaq. Hər bir addımda müqayisə olunan elementlər tünd qara ilə göstərilib.
Sona qədər sıralama üçün 3 keçid lazımdır.
Birinci keçid:
( 5 1 4 2 8 )
→
{\displaystyle \to }
( 1 5 4 2 8 ), Burada alqoritm ilk iki elementi müqayisə edir və 5>1 olduğu üçün 5 ilə 1-in yerini dəyişir.
( 1 5 4 2 8 )
→
{\displaystyle \to }
( 1 4 5 2 8 ), 5 > 4 olduğu üçün
( 1 4 5 2 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 > 2 olduğu
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 ), 5 < 8, heç bir dəyişiklik olmur.
İkinci keçid:
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 4 2 5 8 )
( 1 4 2 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 ), 4 > 2 olduğu üçün
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Hal - hazırda massiv artma sırasına görə sıralanıb (nizamlanıb). Amma alqoritm bunun belə olduğunu bilmədiyi üçün elementlərin yerini dəyişmədən birdaha elementləri müqayisə edəcək.
Üçüncü keçid:
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 )
→
{\displaystyle \to }
( 1 2 4 5 8 )
Python dilində implementasiya aşağıdakı kimi olar.