Fişer Tənliyi

Fişer — soyad. Bobbi Fişer — ABŞ şahmatçısı. Emil Fişer — Almaniya kimyaçısı İrvinq Fişer — amerikalı iqtisadçı Ariya Fişer — Birləşmiş Ştatları təmsil edən su poloçusu. Makenzi Fişer — Birləşmiş Ştatları təmsil edən su poloçusu.

Davamlılıq tənliyi, axdığı boru içərisindəki duruların (mayelərin) axını, onu qoruyub saxlayan bir tənlikdir. Kütlə, enerji, impuls, elektrik yükü və digər təbii miqdarlar lazımi şəraitdə saxlanıldığı üçün müxtəlif fiziki hadisələri davamlılıq tənliyi ilə təsvir etmək olar. == Sıxılmış durular için davamlılıq tənliyi == ρ 1 ⋅ V 1 ⋅ A 1 = ρ 2 ⋅ V 2 ⋅ A 2 {\displaystyle \rho _{1}\cdot \mathbf {V} _{1}\cdot \mathbf {A} _{1}=\rho _{2}\cdot \mathbf {V} _{2}\cdot \mathbf {A} _{2}} burada; ρ {\displaystyle \rho \,} : Sıxlıq , V {\displaystyle \mathbf {V} } Durunun sürəti , A {\displaystyle \mathbf {A} } : Məhdud (Enkesit) vektorial sahədir . == Sıxılmayan durular için davamlılıq tənliyi == V 1 ⋅ A 1 = V 2 ⋅ A 2 {\displaystyle \mathbf {V} _{1}\cdot \mathbf {A} _{1}=\mathbf {V} _{2}\cdot \mathbf {A} _{2}} burada; V {\displaystyle \mathbf {V} } Durunun sürəti , A {\displaystyle \mathbf {A} } : Məhdud (Enkesit) vektorial sahədir .

Diofant tənliyi — adını e.ə III əsrdə yaşadığı təxmin edilən qədim yunan riyaziyyatçısı Diofantdan alan dəyişənləri və əmsalları tam ədəd olan tənlik. Diofant "Hesab" adlı yalnız 6 cildi günümüzə gəlib-çatan əsərində 130 tənliyi və onların həllini qeyd etmişdir. == Xətti Diofant tənlikləri == Sadə xətti tənlikdə nümunələr aşağıdakı kimi verilə bilər; Nümunə 1.1 x + y = 1 {\displaystyle x+y=1} Bu bərabərlikdə hər bir x qiyməti üçün tək bir y həlli var. ( y = 1 − x {\displaystyle y=1-x} ). Bu bərabərliyin həll çoxluğu; (X, 1 − X) şəklindədir hər X ∈ Z üçün Nümunə 1.2 x + 2 y = 1 {\displaystyle x+2y=1} Bu dəfə x-in hər hansı bir tam ədəd ola bilməyəcəyi, lakin sadəcə tək ədəd ola biləcəyi görülür ( x = 1 − 2 y {\displaystyle x=1-2y} ). Bu bərabərliyin həll çoxluğu; (1-2y, y) şəklindədir hər y ∈ Z üçün Nümunə 1.3 3 x + 6 y = 1 {\displaystyle 3x+6y=1} Bu bərabərliyin həlli boş çoxluqdur. Hər x {\displaystyle x} və y {\displaystyle y} tam ədəd seçimi üçün bu tənliyin sol tərəfi həmişə 3-cü qüvvət olduğu halda sağ tərəfi heç vaxt 3-cü qüvvətdən ola bilməz. === Ümumi xətti Diofant tənliyi === a x + b y = c {\displaystyle ax+by=c} şəklindədir. Burada a, b və c tam əmsallar x {\displaystyle x} və y {\displaystyle y} tam ədəd dəyişənləridir. == Digər nümunələr == === Pifaqor teoremi === Ümumi bir nümunə Pifaqor tənliyidir (Bax: Pifaqor teoremi) Nümunə 2.1.1 x 2 + y 2 = z 2 {\displaystyle x^{2}+y^{2}=z^{2}\,} Burada x , y , z {\displaystyle x,y,z} tam ədədləri düzbucaqlı üçbucağın kənar tərəflərini təmsil etdiyi üçün Pifaqor üçlüyü olaraq da adlandırılır.

Diofant tənliyi — adını e.ə III əsrdə yaşadığı təxmin edilən qədim yunan riyaziyyatçısı Diofantdan alan dəyişənləri və əmsalları tam ədəd olan tənlik. Diofant "Hesab" adlı yalnız 6 cildi günümüzə gəlib-çatan əsərində 130 tənliyi və onların həllini qeyd etmişdir. == Xətti Diofant tənlikləri == Sadə xətti tənlikdə nümunələr aşağıdakı kimi verilə bilər; Nümunə 1.1 x + y = 1 {\displaystyle x+y=1} Bu bərabərlikdə hər bir x qiyməti üçün tək bir y həlli var. ( y = 1 − x {\displaystyle y=1-x} ). Bu bərabərliyin həll çoxluğu; (X, 1 − X) şəklindədir hər X ∈ Z üçün Nümunə 1.2 x + 2 y = 1 {\displaystyle x+2y=1} Bu dəfə x-in hər hansı bir tam ədəd ola bilməyəcəyi, lakin sadəcə tək ədəd ola biləcəyi görülür ( x = 1 − 2 y {\displaystyle x=1-2y} ). Bu bərabərliyin həll çoxluğu; (1-2y, y) şəklindədir hər y ∈ Z üçün Nümunə 1.3 3 x + 6 y = 1 {\displaystyle 3x+6y=1} Bu bərabərliyin həlli boş çoxluqdur. Hər x {\displaystyle x} və y {\displaystyle y} tam ədəd seçimi üçün bu tənliyin sol tərəfi həmişə 3-cü qüvvət olduğu halda sağ tərəfi heç vaxt 3-cü qüvvətdən ola bilməz. === Ümumi xətti Diofant tənliyi === a x + b y = c {\displaystyle ax+by=c} şəklindədir. Burada a, b və c tam əmsallar x {\displaystyle x} və y {\displaystyle y} tam ədəd dəyişənləridir. == Digər nümunələr == === Pifaqor teoremi === Ümumi bir nümunə Pifaqor tənliyidir (Bax: Pifaqor teoremi) Nümunə 2.1.1 x 2 + y 2 = z 2 {\displaystyle x^{2}+y^{2}=z^{2}\,} Burada x , y , z {\displaystyle x,y,z} tam ədədləri düzbucaqlı üçbucağın kənar tərəflərini təmsil etdiyi üçün Pifaqor üçlüyü olaraq da adlandırılır.

Dreyk tənliyi — qalaktikada bizimlə əlaqəyə girmək ehtimalı olan sivilizasiyaların sayını hesablamağa imkan verən riyazi formul. Formul aşağıdakı kimidir: N = R ⋅ f p ⋅ n e ⋅ f l ⋅ f i ⋅ f c ⋅ L {\displaystyle N=R\cdot f_{p}\cdot n_{e}\cdot f_{l}\cdot f_{i}\cdot f_{c}\cdot L} burada, N {\displaystyle ~N} — əlaqəyə girməyə hazır olan sivilizasiyaların sayı; R {\displaystyle ~R} — il ərzində bizim qalaktikada yaranan ulduzların sayı; f p {\displaystyle ~f_{p}} — planetləri olan ulduzların xüsusi çəkisi; n e {\displaystyle ~n_{e}} — sivilizasiyanın yaranması üçün müvafiq şəraitə malik olan planetlərin və peyklərin sayı; f l {\displaystyle ~f_{l}} — müvafiq şəraitə malik olan planetdə həyatın yaranması ehtimalı; f i {\displaystyle ~f_{i}} — həyat olan planetdə şüurlu varlıqların yaranma ehtimalı; f c {\displaystyle ~f_{c}} — əlaqəyə hazır olan və əlaqəyə girmək istəyən şüurlu sakinlərə malik planetlərlə, şüurlu sakinləri olan planetlərin sayına nisbəti; L {\displaystyle ~L} — bu sivilizasiyaların ömür müddəti. Formul Kaliforniyanın Santa-Kruz Universitetinin astronomiya və astrofizika professoru Frenk Donald Dreyk tərəfindən 1960-cı ildə təklif olunmuşdur. Onun 1961-ci ildə ehtimal olunan rəqəmlər əsasında apardığı hesablama aşağıdakı kimi olmuşdur. R = 10/il (ildə 10 ulduz yaranır) fp = 0.5 (ulduzların yarısının planetləri var) ne = 2 (sitemdə orta hesabla 2 planet həyat üçün yararlıdır) fl = 1 (əgər həyatın yaranma ehtimalı varsa, o mütləq yaranır) fi = 0.01 (həyatın şüurlu formayadək inkişaf etməsi ehtimalı – 1 %) fc = 0.01 (sivilizasiyaların 1 %-i əlaqə yaratmaq imkanına malik olacaq və əlaqə qurmaq istəyəcək) L = 10 000 il (texniki cəhətdən inkişaf etmiş sivilizasiya 10000 il mövcud olur) Bu təxmini hesablamaya əsasən N = 10 × 0,5 × 2 × 1 × 0,01 × 0,01 × 10000 = 10. Tənlikdəki göstəricilərdən yalnız R {\displaystyle ~R} və f p {\displaystyle ~f_{p}} astronomiyanın indiki inkişaf səviyyəsində müəyyən qədər dəqiq müəyyənləşdirilə bilər. Digər göstəricilərin müəyyənləşdirilməsi mümkün olmadığından Dreyk tənliyi kəskin tənqidlərlə qarşılaşmışdır.

Koşi ötürmə tənliyi Optikada müəyyən bir şəffaf material üçün işığın sınma indeksi və dalğa uzunluğu arasında empirik əlaqə . Adını 1837-ci ildə təyin edən riyaziyyatçı Oqüsten Koşinin şərəfinə almışdır. == Tənlik == Koşi tənliyinin ən ümumi forması n ( λ ) = A + B λ 2 + C λ 4 + ⋯ , {\displaystyle n(\lambda )=A+{\frac {B}{\lambda ^{2}}}+{\frac {C}{\lambda ^{4}}}+\cdots ,} burada n sınma əmsalıdır, λ dalğa uzunluğu, A, B, C və s., tənliyi məlum dalğa uzunluqlarında ölçülmüş sındırma göstəricilərinə uyğunlaşdırmaqla material üçün müəyyən edilə bilən əmsallardır . Əmsallar adətən mikrometrlərdə vakuum dalğa uzunluğu (materialın daxilində olan λ/n kimi deyil) kimi λ üçün göstərilir. Adətən, tənliyin ilk iki həddindən istifadə etmək kifayətdir: n ( λ ) = A + B λ 2 , {\displaystyle n(\lambda )=A+{\frac {B}{\lambda ^{2}}},} burada A və B əmsalları tənliyin bu forması üçün xüsusi olaraq təyin edilir. Ümumi optik materiallar üçün əmsallar cədvəli aşağıda göstərilmişdir: işıq-maddə qarşılıqlı əlaqəni əsaslandıran Koşinin bu tənliyi sonradan yanlış olduğu məlum oldu. Xüsusilə, tənlik yalnız görünən dalğa uzunluğu bölgəsində normal dispersiya bölgələri üçün keçərlidir. İnfraqırmızı dalğalarda tənlik qeyri-dəqiq olur və anomal dispersiya bölgələrini təmsil edə bilmir. Buna baxmayaraq, onun riyazi sadəliyi onu bəzi tətbiqlərdə faydalı edir. Zelmeyer tənliyi anomal dispersiv bölgələri əhatə edən və ultrabənövşəyi, görünən(400-700 nm dalğa uzunluqlu şüalar) və infraqırmızı spektrdə materialın sındırma indeksini daha dəqiq modelləşdirən Koşinin çalışmasının genişləndirilmiş formasıdır.

Laplas tənliyi riyaziyyatda və fizikada ikitərtibli xüsusi törəməli diferensial tənlikdir. Xüsusiyyətləri ilk dəfə Pyer Simon Laplas tərəfindən tətqiq edildiyinə görə onun adını daşıyır. Tənliyin yazılışı aşağıdaki kimidir: ∇ 2 f = 0 və ya Δ f = 0 , {\displaystyle \nabla ^{2}\!f=0\qquad {\mbox{və ya}}\qquad \Delta f=0,} Burada Δ = ∇ ⋅ ∇ = ∇ 2 {\displaystyle \Delta =\nabla \cdot \nabla =\nabla ^{2}} Laplas operatoru, ∇ ⋅ {\displaystyle \nabla \cdot } divergensiya operatoru, ∇ {\displaystyle \nabla } qradiyent operatoru və f ( x , y , z ) {\displaystyle f(x,y,z)} isə iki dəfə diferensiallana bilən həqiqi qiymətli funksiyadır. Belə ki, Laplas operatoru skalyar bir funksiyanı başqa skalyar funksiyaya inkas etdirir. Sağ tərəfdə h ( x , y , z ) {\displaystyle h(x,y,z)} funksiyası təyin olunarsa, onda Laplas tənliyi aşağıdaki kimi verilir: Δ f = h . {\displaystyle \Delta f=h.} Buna Puasson tənliyi, Laplas tənliyinin ümumiləşdirilməsi deyilir. Laplas və Poisson tənlikləri eliptik xüsusi törəməli diferensial tənliklərin ən sadə nümunələridir. Laplas tənliyi, həmçiin Helmholtz tənliyinin xüsusi bir haldır. Laplas tənliyinin həllərinin ümumi nəzəriyyəsi potensial nəzəriyyə olaraq bilinir. Laplas tənliyinin həlli fizikanın bir çox sahələrində, xüsusən elektrostatikada, qravitasiya və maye dinamikasında mühüm əhəmiyyət daşıyan harmonik funksiyalardır.

y ′ + a ( x ) y + b ( x ) y 2 + c ( x ) = 0 {\displaystyle y^{\prime }+a(x)y+b(x)y^{2}+c(x)=0} ( ∗ ) {\displaystyle (*)} şəklində tənliyə Rikkati tənliyi deyilir. Rikkati tənliyi b ( x ) = 0 {\displaystyle b(x)=0} olduqda xətti, c ( x ) = 0 {\displaystyle c(x)=0} olduqda isə Bernulli tənliyinə çevrilir. Rikkati tənliyinin hər hansı y 1 ( x ) {\displaystyle y_{1}(x)} xüsusi həlli məlum olduqda y ( x ) = y 1 ( x ) + z ( x ) {\displaystyle y(x)=y_{1}(x)+z(x)} əvəzləməsi vasitəsilə Bernulli tənliyinə gətirlir. Ümumi halda, Rikkati tənliyi kvadraturaya gətirilə bilmir, yəni həll etmək olmur. Xüsusi halda: b d x d t = x 2 + a t α , ( ∗ ∗ ) {\displaystyle b{\frac {dx}{dt}}=x^{2}+at^{\alpha },\quad (**)} haradakı α , a , b ≠ 0 {\displaystyle \alpha ,\,a,\,b\neq 0} —sabiti, ilk dəfə italyan riyaziyyatçısı tədqiq etmişdir Yakopo Françesko Rikkati və ailələrini Bernulli . α = 4 n / ( 1 − 2 n ) , n ∈ N , {\displaystyle \alpha ={4n}/{(1-2n)},\ n\in \mathbb {N} ,} или α = − 2 {\displaystyle \alpha =-2} Jozef Liuvill (1841)isbat etmişdir. ( ∗ ) {\displaystyle (*)} şəkildə ümumi Rikkati tənliyi , ( ∗ ∗ ) {\displaystyle (**)} — isə xüsusi Rikkati tənliyi adlanır. y ′ + m ( x ) ( A y + B y 2 + C ) = 0 {\displaystyle y^{\prime }+m(x)(Ay+By^{2}+C)=0} olduqda dəyişənlərinə ayrılan, y ′ + A y x + B ( y x ) 2 + C = 0 {\displaystyle y^{\prime }+A{\frac {y}{x}}+B\left({\frac {y}{x}}\right)^{2}+C=0} olduqda bircins, y ′ + A y x + B ( y ) 2 + C x 2 = 0 {\displaystyle y^{\prime }+A{\frac {y}{x}}+B(y)^{2}+{\frac {C}{x^{2}}}=0} olduqda ümumiləşmiş bircns tənliyə çevrilir. y ′ + 2 y e x − y 2 = e 2 x + e x {\displaystyle y^{\prime }+2ye^{x}-y^{2}=e^{2x}+e^{x}} Rikkati tənliyini həll edin. y 1 ( x ) = e x {\displaystyle y_{1}(x)=e^{x}} tənliyin həlli olduğunu bilavasitə yoxlamaq olar.

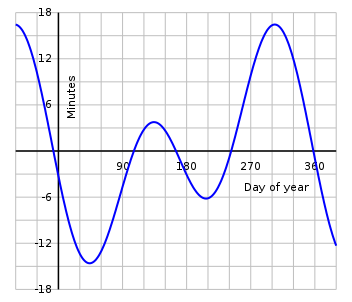
Vaxt tənliyi — eyni an üçün verilmiş coğrafi meridianda orta və həqiqi Günəş vaxtlarının fərqidir. η = T m − T ⊙ = t m − t ⊙ {\displaystyle \eta =T_{m}-T_{\odot }=t_{m}-t_{\odot }} Vaxt tənliyini əslində vaxt düzəlişi adlandırmaq daha doğru olardı, lakin o tarixi olaraq astronomiyaya vaxt tənliyi kimi daxil olmuşdur.

Vəziyyət tənliyi - termodinamikanın makroskopik sistemlərini (temperatur, təzyiq, həcm, kimyəvi potensial və s.) bir-biri ilə əlaqələndirən tənlikdir. f ( P , V , T ) = 0. {\displaystyle f(P,\;V,\;T)=0.} U = U ( T , V ) , {\displaystyle U=U(T,V),} U = U ( T , P ) , {\displaystyle U=U(T,P),} U = U ( V , P ) . {\displaystyle U=U(V,P).} U = U ( S , V ) {\displaystyle U=U(S,\;V)} (daxili enerji üçün kanonik vəziyyət tənliyidir), H = H ( S , P ) {\displaystyle H=H(S,\;P)} (entalpiya üçün kanonik vəziyyət tənliyidir), F = F ( T , V ) {\displaystyle F=F(T,\;V)} (Helmhots enerjisi üçün kanonik vəziyyət tənliyidir), G = G ( T , P ) {\displaystyle G=G(T,\;P)} (Qibbs potensialı üçün kanonik vəziyyət tənliyidir). Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6. Van der Waals, J. D. (1873). On the Continuity of the Gaseous and Liquid States (doctoral dissertation).

Zelmeyer tənliyi müəyyən bir şəffaf mühit üçün sınma indeksi və dalğa uzunluğu arasında empirik əlaqədir . Tənlik işığın mühitdə dispersiyasını təyin etmək üçün istifadə olunur. İlk dəfə 1872-ci ildə Volfqanq Zelmeyer tərəfindən təklif edildi və Augustin Cauchy -nin dispersiyanın modelləşdirilməsi üçün kəşf etdiyi Koşi tənliyinin ümumiləşdirilmiş forması idi. Orijinal və ən ümumi formada Zelmeyer tənliyi aşağıdakı kimi verilir n 2 ( λ ) = 1 + ∑ i B i λ 2 λ 2 − C i {\displaystyle n^{2}(\lambda )=1+\sum _{i}{\frac {B_{i}\lambda ^{2}}{\lambda ^{2}-C_{i}}}} , burada n sınma əmsalı, λ dalğa uzunluğu, Bi və Ci isə eksperimental olaraq müəyyən edilmiş Zelmeyer əmsallarıdır . Bu əmsallar adətən mikrometrlərdə λ üçün göstərilir. Qeyd edək ki, bu λ vakuum dalğa uzunluğudur, yəni materialın daxilində olan λ/n formasında deyil. Tənliyin fərqli forması bəzən müəyyən növ materiallar üçün istifadə olunur, məsələn, kristallar. Cəmin hər həddi, C i {\displaystyle {\sqrt {C_{i}}}} dalğa uzunluğunda Bi -in absorbsiya rezonansını təmsil edir. Məsələn, BK7 şüşəsi üçün aşağıdakı əmsallar ultrabənövşəyi şüada iki, orta infraqırmızı bölgədə isə bir udma rezonansına uyğun gəlir. Hər bir absorbsiya zirvəsinin yaxınında tənlik n2 = ±∞ qeyri-fiziki qiymətləri verir və bu dalğa uzunluğu bölgələrində Helmholtzun tənliyi kimi daha dəqiq dispersiya modelindən istifadə edilməlidir.

Şredinger tənliyi — kvant-mexaniki sistemləri təsvir edən xüsusi törəməli xətti diferensial tənlik; kvant mexanikasının fundamental tənliyi.:1–2 Bu tənlik kvant mexanikasının inkişafında başlıca dönüş nöqtəsi yaratmışdır. Tənlik Ervin Şredingerin adını daşıyır. Şredinger bu tənliyi 1925-ci ildə irəli sürmüş, 1926-cı ildə nəşr etdirmiş, 1933-cü ildə isə bu işinə görə Fizika üzrə Nobel Mükafatı almışdır. Konseptual olaraq Şredinger tənliyi klassik mexanikadakı Nyutonun ikinci qanununun kvant qarşılığıdır. Bir sıra məlum başlanğıc şərtləri nəzərə aldıqda, Nyutonun ikinci qanunu müəyyən bir fiziki sistemin zamanla hansı yolu keçəcəyinə dair riyazi proqnoz verir. Şredinger tənliyi dalğa funksiyasının zamana görə evolyusiyasını, təcrid olunmuş fiziki sistemin kvant-mexaniki xarakteristikasını ifadə edir. Tənlik zaman-evolyusiya operatorunun unitarlığı şərtindən çıxarıla bilər və buna görə də kvant Hamiltonianı olan özü-özünə qoşma operatorun üstlü qiymətiylə əldə olunmalıdır. Şredinger tənliyi kvant-mexaniki sistemləri öyrənmək və proqnozlar vermək üçün yeganə yol deyil. Kvant mexanikasının digər formulyasiyalarına Verner Heyzenberq tərəfindən irəli sürülən matris mexanikası və əsası Riçard Feynman tərəfindən hazırlanmış trayektoriya inteqral formulyasiyası daxildir. Pol Dirak matris mexanikasını və Şredinger tənliyini vahid bir formada birləşdirmişdir.

Şredinger tənliyi — kvant-mexaniki sistemləri təsvir edən xüsusi törəməli xətti diferensial tənlik; kvant mexanikasının fundamental tənliyi.:1–2 Bu tənlik kvant mexanikasının inkişafında başlıca dönüş nöqtəsi yaratmışdır. Tənlik Ervin Şredingerin adını daşıyır. Şredinger bu tənliyi 1925-ci ildə irəli sürmüş, 1926-cı ildə nəşr etdirmiş, 1933-cü ildə isə bu işinə görə Fizika üzrə Nobel Mükafatı almışdır. Konseptual olaraq Şredinger tənliyi klassik mexanikadakı Nyutonun ikinci qanununun kvant qarşılığıdır. Bir sıra məlum başlanğıc şərtləri nəzərə aldıqda, Nyutonun ikinci qanunu müəyyən bir fiziki sistemin zamanla hansı yolu keçəcəyinə dair riyazi proqnoz verir. Şredinger tənliyi dalğa funksiyasının zamana görə evolyusiyasını, təcrid olunmuş fiziki sistemin kvant-mexaniki xarakteristikasını ifadə edir. Tənlik zaman-evolyusiya operatorunun unitarlığı şərtindən çıxarıla bilər və buna görə də kvant Hamiltonianı olan özü-özünə qoşma operatorun üstlü qiymətiylə əldə olunmalıdır. Şredinger tənliyi kvant-mexaniki sistemləri öyrənmək və proqnozlar vermək üçün yeganə yol deyil. Kvant mexanikasının digər formulyasiyalarına Verner Heyzenberq tərəfindən irəli sürülən matris mexanikası və əsası Riçard Feynman tərəfindən hazırlanmış trayektoriya inteqral formulyasiyası daxildir. Pol Dirak matris mexanikasını və Şredinger tənliyini vahid bir formada birləşdirmişdir.

Emil Fişer (9 oktyabr 1852[…] – 15 iyul 1919[…], Berlin, Almaniya Federativ Respublikası) — Almaniya kimyaçısı, 1902-ci il Kimya üzrə Nobel mükafatının laureatı. == Həyatı == O, 1852-ci ildə Almaniyanın Oyskirxen şəhərində dünyaya gəlmişdir. Bonn gimnaziyasını fərqlənmə diplomu ilə bitirmiş, oradakı universitetinə daxil olmuşdur. Dövrün məşhur alimləri-Fridrix Kekule, Avqust Kundt və Paul Qrotdan dərs almışdır. Müəllimi Kekulenin təsirilə kimyadan ayrılıb fizika sahəsinə keçsə də, 1872-ci ildə Strasburq Universitetində təhsilini davam etdirərkən Fişer yenidən kimya ilə maraqlanmağa başlamış, keçirdiyi müxtəlif təcrübələr nəticəsində fenilhidrazini (ətirli hidrazinlər qrupuna aiddir) ixtira edərək məşhurlaşmışdır. 22 yaşında elmlər doktoru adına layiq görülmüş və Strasburq Universitetində müəllim kimi fəaliyyətə başlamışdır. == Fəaliyyəti == Bir müddət burada çalışdıqdan sonra Münhen Universitetinə təyinat almış, burada bir sıra təcrübələr aparmışdır. Üzvi boyaların quruluşunu öyrənən alim onları fenilhidrazinin köməyilə araşdırmışdır. Uzun müddət Münhendə çalışdıqdan sonra Erlangen Universitetində kimya professoru vəzifəsinə keçmişdir. Orada da elmi tədqiqatlarını davam etdirən Fişer kofein, teobromin, quanin və sidik turşusu kimi üzvi birləşmələr üzərində təcrübələr aparmışdır.

Fişer effekti inflyasiya ilə nominal faiz dərəcəsi arasındakı əlaqəni əks etdirir. İqtisadiyyatda iki faiz dərəcəsi fərqləndirilir: nominal faiz dərəcəsi və real faiz dərəcəsi. Nominal faiz dərəcəsi bankdan və ya digər maliyyə qurumundan verilən kreditlər üzərində qoyulan faiz dərəcəsidir. Real faiz dərəcəsi isə inflyasiya nəticəsində qaytararılacaq pul miqdarında baş verən dəyər azalmasını nəzərə alan faiz dərəcəsidir. Bu iki göstərici bir-birindən inflyasiya səviyyəsi qədər fərqlənirlər: (1+i)=(1+r) (1+ π) r - real faiz dərəcəsi; i -nominal faiz dərəcəsi; π -inflyasiya dərəcəsi. Bu şəkildə yazılan tənlik iqtisadçı İrving Fişerin (1867–1947) xatirəsinə Fişer tənliyi adlanır. Bu tənlikdən görünür ki, nominal faiz dərəcəsinin dəyişməsinə iki amil təsir göstərir: real faiz dərəcəsi və inflyasiya. Miqdar qanununa və Fişer tənliyi əsasında, monetar böyümənin nominal faiz dərəcsinə necə təsir etdiyini müəyyən etmək mümkündür. Miqdar qanununa görə, pulun miqdarındakı 1%-lik artım inflyasiya dərəcəsini 1% artırır. Fişer tənliyinə görə, inflyasiya dərəcəsindəki 1%-lik artım nominl faiz dərəcəsini təxminən 1% artırır.

Sternbergia vernalis (lat. Sternbergia vernalis) — bitkilər aləminin qulançarçiçəklilər dəstəsinin nərgizçiçəyikimilər fəsiləsinin şternbergiya cinsinə aid bitki növü. == Sinonimləri == === Homotipik sinonimləri === Amaryllis vernalis Mill. === Heterotipik sinonimləri === Amaryllis lutea M.Bieb. Oporanthus fischerianus Herb. Sternbergia fischeriana (Herb.) Roem. Sternbergia fischeriana subsp. hissarica (Kapinos) Artjush. Sternbergia fischeriana f.

Hans Fişer (alm. Hans Fischer;‎ 27 iyul 1881[…], Frankfurt-Mayn, Prussiya – 31 mart 1945[…], Münxen) – 1930-cu ildə "Hemin və xlorofilin tərkibi ilə əlaqəli tədqiqatlarına və xüsusilə heminin sintezinə görə" Kimya üzrə Nobel mükafatı laureatı olmuş almaniyalı üzvi kimyaçı. == Həyatı == === Erkən həyatı === Fişer 1881-ci ildə Frankfurtda anadan olub. Ştutqartda ibtidai məktəbi bitirdikdən sonra orta təhsilini Visbadendəki Humanitar Gimnaziyada aldı. Əvvəlcə Lozanna Universitetində, sonra Marburq Universitetində kimya və tibb üzrə təhsil aldı. 1904-cü ildə kimya ixtisasından məzun oldu, 1908-ci ildə isə tibb üzrə doktorluq dərəcəsi aldı. === Kariyerası === Əvvəlcə Münhendəki Tibb Klinikasında, daha sonra Emil Fişerin rəhbərliyi altında Birinci Berlin Kimya İnstitutunda çalışdı. 1911-ci ildə yenidən Münhenə qayıtdı. 1913-cü ildə Münhendəki Fizioloji İnstitutda fiziologiya üzrə lektor olaraq işə başladı. 1916-cı ildə İnsbruk Universitetində Tibbi Kimya professoru oldu və 1918-ci ildə Vyana Universitetinə getdi.

Haynz Fişer (9 oktyabr 1938[…], Qrats) — Avstriya Respublikasının prezidenti. Vyana Universitetində hüquq təhsili alıb. Avstriya Sosial Demokrat Partiyasına qatılıb. 1993-cü ildə Innsbruckta hüquq professoru, 2004-cü ildə prezident olub.

Kerri Fişer (ing. Carrie Fisher; 21 oktyabr 1956[…], Berbank, Kaliforniya və ya ABŞ – 27 dekabr 2016[…], Los-Anceles, Kaliforniya) — ABŞ aktrisası və ssenaristi. == Həyatı == 21 oktyabr 1956-cı ildə Kaliforniya ştatının Los-Anceles şəhərində Eddi Fişer və Debbi Reynoldsun ailəsində doğulub. 2 yaşı olanda ailə dağılmış və ata məşhur aktrisa Elizabet Teylorla evlənmişdir. Uşaqlıqda aktrisa olmaq arzusu olan Kerri "Central School of Spench and Drama"da təhsil aldı. İlk filmi "Şampun" filminə 1975-ci ildə çəkildi. Aktrisanın karyerasında dönüş yaradan film isə 1977-ci ildə çəkilən Ulduz müharibələri filmində "Şahzadə Leya" obrazı oldu. Daha sonra 1980-ci ildə "Cazmen Qardaşlar" filmində rol aldı. 1990-cı ildə "Postcards from the Edge" filminin sserisini yazmışdır. Kerri Fişer 27 dekabr 2016-cı ildə Londondan qayıdarkən təyyarədə infarkt keçirmişdir.

Lui Fişer (ing. Louis Fischer; 29 fevral 1896, Filadelfiya, Pensilvaniya – 15 yanvar 1970, Prinstom, Nyu-Cersi) — ABŞ tarixçisi, jurnalisti və publisisti. 1923–1937-ci illərdə müxtəlif ABŞ və Birləşmiş Krallıq qəzetlərinin Moskva təmsilçisi olmuşdu. SSRİ haqqında çoxsaylı kitabların, o cümlədən Lenin və Stalinin bioqrafiyalarının müəllifidir. 1965-ci ildə Tarix və Bioqrafiya üzrə Milli Kitab Mükafatını qazanmışdır. == İstinadlar == == Əlavə ədəbiyyat == Wolf, Markus. Die Troika: Geschichte eines Nichtgedrehten Films [The Troika: The Story of a Non-Made Film] (alman). Aufbau-Verlag. January 1, 1989. ISBN 978-3546498395.

Makenzi Fişer (d. 29 mart 1997) — Birləşmiş Ştatları təmsil edən su poloçusu. == Karyerası == Makenzi Fişer, ABŞ yığmasının heyətində 2016-cı ildə Braziliyanın Rio-de-Janeyro şəhərinin ev sahibliyində baş tutan XXXI Yay Olimpiya Oyunlarında mübarizə apardı. Final görüşündə İtaliya yığmasını 12:5 hesabı ilə məğlub edən ABŞ yığması, Rio-de-Janeyro Olimpiadasının qızıl medalına sahib oldu.

Eugen Fischer (5 iyul 1874, Karlsrue – 9 iyul 1967[…], Frayburq-im-Braysqau, Baden-Vürtemberq) alman tibb, antropologiya və yevgenika professoru və Nasist Partiyasının üzvü idi. O, Kayzer Vilhelm adına Antropologiya, İnsan İrsiyyəti və Yevgenika İnstitutunun direktoru, həmçinin Berlindəki Frederik Uilyam Universitetinin rektoru olmuşdur. Fişerin ideyaları Nasist Partiyasının alman irqi üstünlüyünə olan inamının düzgünlüyünü ifadə edən 1935-ci il Nürnberq qanunlarını lazımi informasiya ilə təmin etdi. Adolf Hitler 1923-cü ildə həbsxanada olarkən Fişerin əsərlərini oxumuş və özünün “Mein Kampf” (Mənim Mübarizəm) manifestində saf ari cəmiyyəti idealını dəstəkləmək üçün Fişerin qəzəbli fikirlərindən istifadə etmişdir. Fişer 1874-cü ildə Karlsruedə, Baden Böyük Hersoqluğunda anadan olub. Berlin, Frayburq və Münhendə tibb, folklorşünaslıq, tarix, anatomiya və antropologiya üzrə təhsil alıb. 1918-ci ildə Frayburq Universitetinin tərkibində olan Frayburq Anatomiya İnstitutuna daxil oldu. 1927-ci ildə Fişer Kaiser Wilhelm Antropologiya, İnsan İrsiyyəti və Yevgenika İnstitutunun (KWI-A) direktoru oldu, bu rolu əvvəlki il Ervin Baur ona tövsiyə etmişdi. 1933-cü ildə Fişer Almaniya universitetlərinin və liseylərinin professorlarının Adolf Hitlerə və Nasional Sosialist Dövlətinə sadiq qalacağına söz verdi. 1933-cü ildə Adolf Hitler onu Berlindəki Frederik Uilyam Universitetinin, indiki Humboldt Universitetinin rektoru təyin etdi.

Robert "Bobbi" Ceyms Fişer (ing. Robert James "Bobby" Fischer) 9 mart 1943[…], Çikaqo, İllinoys[…] – 17 yanvar 2008, Reykyavik[…]) — ABŞ şahmatçısı. Şahmat üzrə 11-ci dünya çempionu (1972–1975). Fischer 1943-cü il martın 9-da Çikaqoda yəhudi ailəsində anadan olmuşdur. Valideynləri Almaniya (atası) və İsveçrədəndir (anası). ABŞda siyasi baxışlarına görə təqib olunan kommunist, antifaşist atası Hans-Herhardt Fişer (Gerardo Liebscher kimidə tanınır) ikinci dünya müharibəsi bitdikdən sonra Almaniyaya qayıtmalı olur. (SSRİ xüsusi kəşfiyyat orqanı üzvi, bəzi mənbələrə görə). Robertin atası haqda çox az məlumatı vardı. Yalnız adının Herhardt olmasını bilirdi. Ona macar yəhudilərindən olan Pol Nemeni atalıq edib.

Robert "Bobbi" Ceyms Fişer (ing. Robert James "Bobby" Fischer) 9 mart 1943[…], Çikaqo, İllinoys[…] – 17 yanvar 2008, Reykyavik[…]) — ABŞ şahmatçısı. Şahmat üzrə 11-ci dünya çempionu (1972–1975). Fischer 1943-cü il martın 9-da Çikaqoda yəhudi ailəsində anadan olmuşdur. Valideynləri Almaniya (atası) və İsveçrədəndir (anası). ABŞda siyasi baxışlarına görə təqib olunan kommunist, antifaşist atası Hans-Herhardt Fişer (Gerardo Liebscher kimidə tanınır) ikinci dünya müharibəsi bitdikdən sonra Almaniyaya qayıtmalı olur. (SSRİ xüsusi kəşfiyyat orqanı üzvi, bəzi mənbələrə görə). Robertin atası haqda çox az məlumatı vardı. Yalnız adının Herhardt olmasını bilirdi. Ona macar yəhudilərindən olan Pol Nemeni atalıq edib.

Stenli Fişer (ivr. ‏סטנלי פישר‏‎; 15 oktyabr 1943) — 2014-2017-ci illərdə Federal Ehtiyat Sisteminin 20-ci sədr müavini vəzifəsində çalışmış İsrail əsilli amerikalı iqtisadçı. Fişer bundan əvvəl 2005-2013-cü illərdə İsrail Mərkəzi Bankının 8-ci sədri vəzifəsində çalışıb. Şimali Rodeziyada (indiki Zambiya) anadan olub, İsrail və ABŞ-də ikili vətəndaşlığa malikdir. O, əvvəllər Beynəlxalq Valyuta Fondunun icraçı direktorunun birinci müavini və Dünya Bankının baş iqtisadçısı vəzifələrində çalışıb. 10 yanvar 2014-cü ildə Prezident Barak Obama Fişeri ABŞ Federal Ehtiyat Sisteminin Rəhbərlər Şurasının sədr müavini vəzifəsinə irəli sürdü. O, Blackrock-da baş məsləhətçidir. 6 sentyabr 2017-ci ildə Stenli Fişer 74-cü doğum gününə az qalmış, 13 oktyabr 2017-ci il tarixindən etibarən şəxsi səbəblərə görə sədr müavini vəzifəsindən istefa verdiyini açıqladı.