düzgün

Düzgün altıbucaqlı
Düzgün altıbucaqlı — altı bucağı olan düzgün çoxbucaqlıdır.
== Xassələri ==
Xarici bucaqların ölçüləri eynidir.
Daxili bucaqların ölçüləri eynidir.
Tərəflərin uzunluqları eynidir.
== Xarici və daxili bucaqları ==
Tərəfləri a olarsa
Xarici bucağı
α
=
360
∘
a
=
360
∘
6
=
60
∘
{\displaystyle \alpha ={\frac {360^{\circ }}{a}}\ ={\frac {360^{\circ }}{6}}\ ={60^{\circ }}}
Daxili bucağı
β
=
180
∘
(
6
−
2
)
a
=
180
∘
⋅
4
6
=
120
∘
{\displaystyle \beta ={\frac {180^{\circ }(6-2)}{a}}={\frac {180^{\circ }\cdot 4}{6}}={120^{\circ }}}
== Diaqonalları ==
Altıbucaqlının diaqonallarının sayı:
n
⋅
(
n
−
3
)
2
{\displaystyle {\frac {n\cdot (n-3)}{2}}}
n= 6 Diaqonalların sayı:9
Tərəfi a olarsa, böyük diaqonalı:d=2a.
== Perimetri ==
P
=
6
⋅
a
{\displaystyle P=6\cdot a}
== Sahəsi ==
S
=
3
2
a
2
cot
π
6
=
3
3
2
a
2
≃
2.59808
a
b
2
.

Düzgün axış
Sıvı dinamikasında, Düzgün axış, (yaxud yarpaqlı axış,laminar axın), (ing. laminar flow) təbəqələrdə hamar(pürüzsüz) yolları izləyən sııvı hissəcikləri ilə xarakterizə olunur, hər təbəqə bitişik təbəqələrdən az və ya çox qarışıq olmadan hamar bir şəkildə hərəkət edir. Aşağı sürətlə sıvı yanal qarışdırmadan axmağa meyl edir və bitişik təbəqələrdə kart oynundaki kimi bir-birinin üstündən sürüşür. Axışın istiqamətinə dik olan kəsişən cərəyanlar yoxdur, qarışıqlar da yoxdur. Düzgün axışda, sıvının hissəciklərinin hərəkəti bərk bir səthə yaxın hissəciklər ilə həmin səthə paralel düz xətlərdə hərəkət edir. Düzgün axış yüksək impuls yayılması və aşağı impuls konveksiyası ilə xarakterizə olunan bir axın rejimidir.
== Reynolds ədədi ilə əlaqəsi ==
Reynolds ədədinin xüsusi hesablanması və düzgün axışının meydana gələcəyi dəyərlər axın sisteminin həndəsəsindən və axın davranışıdan asılı olacaqdır. Ümumi nümunə, bir boru vasitəsilə sıvının axındır. Reynolds ədədi aşağıdakı kimi təyin olur.
R
e
=
ρ
u
D
H
μ
=
u
D
H
ν
=
Q
D
H
ν
A
,
{\displaystyle \mathrm {Re} ={\frac {\rho uD_{\text{H}}}{\mu }}={\frac {uD_{\text{H}}}{\nu }}={\frac {QD_{\text{H}}}{\nu A}},}
Burada:
DHborunun hidravlik diametridir (m);
Qdebidir (m3/s);
A,borunun kəsişmə sahəsi (m2);
usıvının orta sürətidir (SI vahidləri: m / s);
μsıvının dinamik özlülüğüdür (Pa·s = N·s/m2 = kg/(m·s));
νsıvının kinematik özlülüğüdür (ν = μ/ρ(m2/s);
ρsıvının sıxlığıdır (kg/m3).
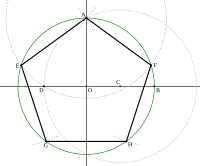
Düzgün beşbucaqlı
Düzgün beşbucaqlı-beş bucağı olan düzgün çoxbucaqlıdır.
== Beşbucaqlının qurulması ==
== Xassələri ==
Xarici bucaqların ölçüləri eynidir.
Daxili bucaqların ölçüləri eynidir.
Tərəflərin uzunluqları eynidir.
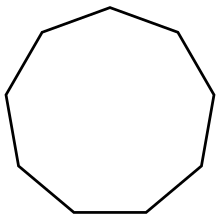
Düzgün doqquzbucaqlı
== Xassələri ==
Xarici bucaqların ölçüləri eynidir.
Daxili bucaqların ölçüləri eynidir.
Tərəflərin uzunluqları eynidir.
Xarici bucaqlaın cəmi:
=
360
∘
{\displaystyle ={360^{\circ }}}
Beşbucaqlının bir tərəfli a olarsa
== Xarici və daxili bucaqları ==
Xarici bucağı
α
=
360
∘
a
=
360
∘
9
=
40
∘
{\displaystyle \alpha ={\frac {360^{\circ }}{a}}\ ={\frac {360^{\circ }}{9}}\ ={40^{\circ }}}
Daxili bucağı
β
=
180
∘
(
9
−
2
)
a
=
180
∘
⋅
7
9
=
140
∘
{\displaystyle \beta ={\frac {180^{\circ }(9-2)}{a}}={\frac {180^{\circ }\cdot 7}{9}}={140^{\circ }}}
== Diaqonalları ==
Düzgün doqquzbucaqlının sayı
9
⋅
(
9
−
3
)
2
=
27
{\displaystyle {\frac {9\cdot (9-3)}{2}}={27}}
== Sahəsi ==
S
=
9
3
a
2
4
{\displaystyle S={\frac {9{\sqrt {3}}a^{2}}{4}}}
Qeyd: Bu düsturu almaq çox sadədir:
Düzgün doqquzbucaqlı 9 bərabərtərəfli üçbucaqdan təşkil olunduğu üçün bərabərtərəfli üçbucağın sahəsini doqquza vururuq
S
=
3
a
2
4
⋅
9
{\displaystyle S={\frac {{\sqrt {3}}a^{2}}{4}}\cdot {9}}
.

Düzgün onyeddibucaqlı
Düzgün onyeddibucaqlı — onyeddi bucağlı və onyeddi tərəfli olan çoxbucaqlıdır.
== Xüsusiyyətlər ==
Mərkəzi α bucağı
360
∘
17
≈
21,176
47059
∘
{\displaystyle {\frac {360^{\circ }}{17}}\approx 21{,}17647059^{\circ }}
bərabərdir.
Onyeddibucaqlının tərəfinin bu çevrənin radiusunu ilə ifadəsi:
s
=
2
⋅
r
u
⋅
sin
(
α
2
)
≈
r
u
⋅
0,367
5
{\displaystyle s=2\cdot r_{u}\cdot \sin \left({\frac {\alpha }{2}}\right)\approx r_{u}\cdot 0{,}3675}
.
Düzgün onyeddibucaqlını pərgarın və xəttin köməyi ilə qurmaq olar. 1796-cı ildə Qaus tərəfindən sübut edilmişdi. O, mərkəzi bucağın kosinusunun qiymətini tapmışdır.
cos
360
∘
17
=
1
16
(
−
1
+
17
+
2
(
17
−
17
)
+
2
17
+
3
17
−
2
(
17
−
17
)
−
2
2
(
17
+
17
)
)
{\displaystyle \cos {\frac {360^{\circ }}{17}}={\frac {1}{16}}\left(-1+{\sqrt {17}}+{\sqrt {2\left(17-{\sqrt {17}}\right)}}+2{\sqrt {17+3{\sqrt {17}}-{\sqrt {2\left(17-{\sqrt {17}}\right)}}-2{\sqrt {2\left(17+{\sqrt {17}}\right)}}}}\right)}
== Faktlar ==
Qauss vəsiyyətində bildirirdi ki, onun qəbrini düzgün on yeddi bucaqlı formasında yonsunlar. Heykəltəraş bunu etməkdən imtina edərək bildirdi ki, bu çox çətin işdir və elə də dəqiqlik olmayacaq.
1825-ci ildə Yoxannes Erxinqer ilk dəfə 64 gedişli düzgün onyeddibucaqlının qurulmasının ətraflı təsvirini etdi.

Düzgün yeddibucaqlı
Düzgün yeddibucaqlı-yeddi tərəfi olan düzgün çoxbucaqlıdır.
== Xassələri ==
Xarici bucaqların ölçüləri eynidir
Daxili bucaqlarının ölçüləri eynidir
Tərəflərin uzunluqları eynidir
== Diaqonalları ==
Düzgün yeddibucaqlının diaqonallarının sayı
7
⋅
(
7
−
3
)
2
=
14
{\displaystyle {\frac {7\cdot (7-3)}{2}}={14}}
== Perimetri ==
t
{\displaystyle t}
— Düzgün yeddibucaqlıda təfəfi,
R
{\displaystyle R}
— xarixaricinə kəçilmiş radius,
r
{\displaystyle r}
—daxilinə çəkilmiş radius olarsa.
P
=
7
t
=
14
R
sin
π
7
=
14
r
sin
π
7
{\displaystyle P=7t=14R\sin {\frac {\pi }{7}}=14r\sin {\frac {\pi }{7}}}
.

Düzgün çoxbucaqlılar
Düzgün çoxbucaqlılar
Xarici bucaqların ölçüləri eynidir.
Daxili bucaqların ölçüləri eynidir.
Tərəflərin uzunluqları eynidir.

Düzgün üçbucaq
Düzgün üçbucaq, yaxud bərabərtərəfli üçbucaq - bütün tərəfləri bərabər olan üçbucağa deyilir. Tərifdən aydın olur ki, düzgün üçbucaq həm də bərabəryanlı üçbucaqdır.
== Xassələri ==
İstənilən bucaqdan qarşı tərəfə endirilmiş hündürlük, həm median, həm də həmin bucağın tənbölənidir (düstur aşağıda verilmişdir).;
Düzgün üçbucağın bucaqlarının hər biri 60°-dir.
(Teorem: Üçbucaqda istənilən iki tərəfin qiyməti eyni və onlar arasındakı bucaq 60°-dirsə, deməli, bu üçbucaq bərabərtərəflidir/düzgündür)
Tutaq ki,
n
{\displaystyle n}
düzgün üçbucağın tərəfi,
R
{\displaystyle R}
— xaricə çəkilmiş çevrənin radiusu,
r
{\displaystyle r}
isə daxilə çəkilmiş çevrənin radiusudur.
Daxilə çəkilmiş çevrənin onun tərəfi ilə əlaqəsi:
r
=
3
6
n
{\displaystyle r={\frac {\sqrt {3}}{6}}n}
.
Xaricə çəkilmiş çevrənin onun tərəfi ilə əlaqəsi:
R
=
3
3
n
{\displaystyle R={\frac {\sqrt {3}}{3}}n}
.
Düzgün üçbucağın perimetri:
P
=
3
n
=
3
3
R
=
6
3
r
{\displaystyle P=3n=3{\sqrt {3}}R=6{\sqrt {3}}r}
.
Düzgün üçbucağın hündürlüyü:
h
=
3
2
n
{\displaystyle h={\frac {\sqrt {3}}{2}}n}
,
Düzgün üçbucağın sahəsi aşağıdakı düsturlarla hesablanır:
S
=
3
4
n
2
=
3
3
4
R
2
=
3
3
r
2
{\displaystyle S={\frac {\sqrt {3}}{4}}n^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}}
.

Düzgün üçbucaqlı
Düzgün üçbucaq, yaxud bərabərtərəfli üçbucaq - bütün tərəfləri bərabər olan üçbucağa deyilir. Tərifdən aydın olur ki, düzgün üçbucaq həm də bərabəryanlı üçbucaqdır.
== Xassələri ==
İstənilən bucaqdan qarşı tərəfə endirilmiş hündürlük, həm median, həm də həmin bucağın tənbölənidir (düstur aşağıda verilmişdir).;
Düzgün üçbucağın bucaqlarının hər biri 60°-dir.
(Teorem: Üçbucaqda istənilən iki tərəfin qiyməti eyni və onlar arasındakı bucaq 60°-dirsə, deməli, bu üçbucaq bərabərtərəflidir/düzgündür)
Tutaq ki,
n
{\displaystyle n}
düzgün üçbucağın tərəfi,
R
{\displaystyle R}
— xaricə çəkilmiş çevrənin radiusu,
r
{\displaystyle r}
isə daxilə çəkilmiş çevrənin radiusudur.
Daxilə çəkilmiş çevrənin onun tərəfi ilə əlaqəsi:
r
=
3
6
n
{\displaystyle r={\frac {\sqrt {3}}{6}}n}
.
Xaricə çəkilmiş çevrənin onun tərəfi ilə əlaqəsi:
R
=
3
3
n
{\displaystyle R={\frac {\sqrt {3}}{3}}n}
.
Düzgün üçbucağın perimetri:
P
=
3
n
=
3
3
R
=
6
3
r
{\displaystyle P=3n=3{\sqrt {3}}R=6{\sqrt {3}}r}
.
Düzgün üçbucağın hündürlüyü:
h
=
3
2
n
{\displaystyle h={\frac {\sqrt {3}}{2}}n}
,
Düzgün üçbucağın sahəsi aşağıdakı düsturlarla hesablanır:
S
=
3
4
n
2
=
3
3
4
R
2
=
3
3
r
2
{\displaystyle S={\frac {\sqrt {3}}{4}}n^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}}
.

Düzgün - çalxantılı axış keçidi
Sıvı dinamikasında düzgün axınının çalxantılı hala gəlməsi düzgün-çalxantılı axış keçidi kimi tanınır. Keçidi xarakterizə edən əsas parametr Reynolds sayısıdır .
Keçid dalbadal bir sıra mərhələlərdən keçən bir proses kimi təsvir olunur. "Keçid axını" hər iki istiqamətə, yəni düzgün-çalxantılı keçidi və ya çalxantılı-düzgün keçidi axışına işləniləbilir.
Proses hər hansı bir sıvı axınına aiddir və əksər hallarda sərhəd təbəqələri için istifadə olunur.
Düzgün olmayan başlanğıc (şahmat)
Şahmat terminlərinin lüğəti — Şahmat ədəbiyyatında tez-tez rast gəlinən əsas şahmat anlayışları və terminləri verilir.
== A ==
Axmaq matı — şahmatda ən tez mümkün olan mat növü.
Alyoxin müdafiəsi
Armaqedon
Avanpost
== B ==
Batareya (şahmat)
== C ==
Cənub qambiti — İlk dəfə olaraq 1867-ci ildə danimarkalı usta Fromen və isveç şahmatçısı Lindek tərəfindən praktikaya tətbiq edilmişdir.
Cinah — Şahmat taxtasının bir hissəsi sol cinah ağlar üçün vəzir, qaralar üçn isə şah cinahı adlandırılır.
== Ç ==
Çevrilən piyada — Sonuncu xanaya çataraq şahdan başqa istənilən fiqura çevrilən piyadaya deyilir.
Çəngəl — Piyadanın və ya atın eyni vaxtda iki fiqura və ya piyadaya hücumu.
== D ==
Daimi şah — "Şah"ların ardıcıl seriyasıdır ki, şah özünə sığınacaq tapa bilmir.
Dəyirman — Topun və filin iştirakı ilə açıq silsilə şahlar elan edən kombinasiyanın adı.
Dəyişmə — Bir-birinə bərabər olan fiqurların dəyişməsi gedişidir.
Düzgün olmayan başlanğıc — Bir sıra az işlənən və nəzəriyyəcə zəif işlədilmiş başlanğıcların (1.d3-Andersson debütü; 1.e3-van Kruysa debütü; 1.c3-Saraqossa başlanğıcı; 1.d3-Mizes başlanğıcı) və adsız başlanğıcların (1.b3, 1.

