HƏNDƏSİ

Həndəsi forma — Yer, miqyas, yönləndirmə və refleksiyanın həndəsi obyektin təsvirindən çıxarıldığı zaman qalan həndəsi məlumatdır. == Haqqında == Yəni forma ətrafında hərəkətin, onun genişlənməsinin, dönməsinin və ya güzgüdə əks olunmasının nəticəsi, ayrı bir forma deyil, orijinal forma ilə eynidir. Eyni formaya malik olan obyektlərin oxşar olduğu deyilir. Bir-birləri ilə eyni miqyasda olduqları təqdirdə, onlara bir-birinə uyğun olan deyilir. Bir çox ikiölçülü həndəsi formalı bir nöqtə və ya birbaşa və ya bağlanmış bir nöqtədə nöqtələri birləşdirən xəttlər, həmçinin nəticələnən daxili nöqtələrlə müəyyən edilə bilər. Belə formalar çoxbucaqlı adlanır və üçbucaqlar, kvadratlar və pentaqonlar daxildir. Digər formalar bir dairə və ya ellips kimi əyri ilə məhdudlaşdıra bilər. Bir çox üçölçülü həndəsi fiqurlar bir sıra şaquli, hündürlüyü birləşdirən xəttlər və bu xətlərin əhatə etdiyi iki ölçülü üzlər, eləcə də yaranan daxili nöqtələrlə müəyyən edilə bilər. Bu cür formlara polihedra deyilir və buraya kublar daxildir, həmçinin tetrahedra kimi piramidalar. Digər üç ölçülü şəkillər ellips və sfera kimi əyri səthlərlə məhdudlaşdıra bilər.

n {\displaystyle n} müsbət a 1 , a 2 , … , a n {\displaystyle a_{1},a_{2},\dots ,a_{n}} ədədinin həndəsi ortası onların hasilinin n {\displaystyle n} dərəcəli hesabi kökünə deyilir: G = a 1 ⋅ a 2 ⋯ a n n {\displaystyle G={\sqrt[{n}]{a_{1}\cdot a_{2}\cdots a_{n}}}} və ya G = ∏ i = 1 n a i n {\displaystyle G={\sqrt[{n}]{\prod \limits _{i=1}^{n}a_{i}}}} . İki ədədin həndəsi ortası onlarla orta mütənasib də deyilir. Bir neçə ədədin həndəsi ortası digər ortalar kimi onların ən kiçiyi ilə ən böyüyü arasında olur. Bir neçə ədədin həndəsi ortası onların qüvvət ortasının xüsusi halıdır. == Ədəbiyyat == 1. M.Mərdanov, S.Mirzəyev, Ş. Sadıqov Məktəblinin riyaziyyatdan izahlı lüğəti. Bakı 2016, "Radius nəşriyyatı", 296 səh.

Həndəsi qurmalar — yaxud Qurma məsələləri müxtəlif alətlərin (birtərəfli riyazi xətkeş, ikitərəfli xətkeş, pərgar, düz bucaq modeli və s. alətlər) köməyi ilə müxtəlif şərtləri ödəyən həndəsi fiqurların qurulmasıdır. Həndəsənin həndəsi qurmaların üsullarını öyrənən bölməsinə konstruktiv həndəsə deyilir. Qurma məsələləri həm Evklid həndəsəsində, həm də başqa həndəsələrdə (Sferik həndəsədə, Lobaçevski həndəsəsində və s.) öyrənilir. Bu məsələlərə həm müstəvi üzərində, həm də fəzada baxılır. Qurmanın klassik alətləri pərgar və xətkeşdir. Lakin, təkcə, pərgarla (Mor-Maskeroni qurmaları), təkcə, birtərəfli xətkeşlə (Şteyner qurmaları), təkcə, ikitərəfli xətkeşlə, təkcə, düz bucaqla (düz bucağın modeli) və s. alətlərlə qurmalara da baxılır. Bütün qurma məsələləri Konstruktiv həndəsənin aksiomlarına əsaslanır. Konstruktiv həndəsənin aksiomları ən sadə həndəsi qurmalardır.

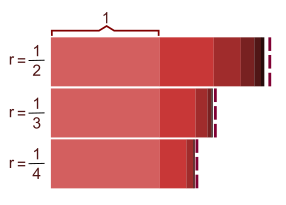
Həndəsi silsilə (bəzən həndəsi ardıcıllıq) — ilk həddi sıfırdan fərqli olmaqla ikincidən başlayaraq hər bir həddi özündən əvvəlki ilə silsilə vuruğu adlanan sıfırdan fərqli sabit ədədin hasilinə bərabər olan ədədi ardıcıllıq. Məsələn, 2, 6, 18, 54, … ardıcıllığı silsilə vuruğu 3 olan həndəsi silsilədir. Eynilə 10, 5, 2.5, 1.25, … silsilə vuruğu 1/2 olan həndəsi silsilədir. Həndəsi silsiləyə misal olaraq 2k və 3k kimi sıfırdan fərqli r sabitinin rk qüvvətlərini göstərmək olar. Həndəsi silsilənin ümumi forması belədir a , a r , a r 2 , a r 3 , a r 4 , … {\displaystyle a,\ ar,\ ar^{2},\ ar^{3},\ ar^{4},\ \ldots } burada r ≠ 0 silsilə vuruğu, a ≠ 0 isə ardıcıllığın başlanğıc qiymətinə bərabər olan əmsaldır. Silsilə və sıra arasındakı arasındakı fərq ondan ibarətdir ki, silsilə ardıcıllıq, sıra isə cəmdir. == Elementar xassələr == İlk həddi a = a1, silsilə vuruğu r olan həndəsi silsilənin n-ci həddi aşağıdakı kimi verilir: a n = a r n − 1 {\displaystyle a_{n}=a\,r^{n-1}} Belə həndəsi silsilə rekurrent münasibətə uyğundur: hər bir n ≥ 2 {\displaystyle n\geq 2} tam ədədi üçün a n = r a n − 1 {\displaystyle a_{n}=r\,a_{n-1}} Ümumiyyətlə, verilmiş ardıcıllığın həndəsi olub-olmadığını yoxlamaq üçün sadəcə ardıcıllığın bütün hədlərinin eyni silsilə vuruğuna malik olub-olmadığını yoxlamaq kifayətdir. Silsilə vuruğu mənfi olarsa, işarəsi müsbət və mənfinin arasında dəyişən ədədi ardıcıllıq alınar. Misal üçün 1, −3, 9, −27, 81, −243, … silsilə vuruğu −3 olan həndəsi silsilədir. Həndəsi silsilənin davranışı silsilə vuruğunun qiymətindən asılıdır.

Həndəsi çevrilmələr — müstəvinin həndəsi çevrilmələri müstəvinin özünə qarşılıqlı birqiymətli inikasıdır. Ən mühüm həndəsi çevrilmə hərəkətdir. Yəni nöqtələr arasında məsafələri saxlayan həndəsi çevrilmələr. Hərəkət fiqurların bərabərliyi ilə əlaqədardır. "İki fiqurdan birini digərinə çevirən hərəkət varsa, onlara bərabər fiqurlar deyilir. Bu tərifi Evklidin özü də qəbul etmişdir". (Bərk fiqurları bütün nöqtələrinin üst-üstə düşməsi şərti ilə bir-birinin üzərinə qoymaq əslində hərəkətdir). Hərəkətlərdən bəziləri müstəvinin nöqtələrinin qarşılıqlı vəziyyətini saxlayır (paralel köçürmə və dönmə), bəziləri isə saxlamır (ox simmetriyası). Həndəsi çevrilmələr növbəti mühüm qrupu oxşarlıq çevrilmələridir. Onların ən sadəsi homotetiyadır.

Həndəsi nisbətlər qanunu Bu qanun David Dalton (1803) tərəfindən kəşf olunmuşdur: Əgər iki element bir-birilə bir neçə birləşmə əmələ gətirirsə, bunlardan birinin eyni kütləsinə düşən digər elementin kütlələri nisbəti sadə tam ədədlərin nisbəti kimidir. Məsələn, CO2 ilə CO birləşmələrində karbonla oksigenin kütlələri nisbəti 12:32 və 12:16 nisbəti kimidir. Deməli, karbonun oksigenin sabit kütləsi ilə birləşən kütlələri nisbəti 2:1-ə nisbəti kimidir. Bu qanun əsasında Dalton hidrogenin kütləsini şərti olaraq vahid qəbul edərək elmə nisbi atom kütləsi anlayışını daxil etmişdir. Hal-hazırda isə göstərdiyimiz kimi nisbi atom kütlə vahidi olaraq karbon-12 izotopunun molyar kütləsinin 1/12 qəbul edilmişdir.

Həndəsi qurmalar nəzəriyyəsi — həndəsənin müəyyən alətlərin köməyi ilə həndəsi fiqurların qurulması üsullarını öyrənən bölməsidir. Həndəsi qurmalar təkcə, Evklid həndəsəsində deyil, digər həndəsələrdə də (sferik həndəsədə, proyektiv həndəsədə, Lobaçevski həndəsəsində və s.) öyrənilir. Həndəsi qurmalar təkcə müstəvi üzərində deyil, fəzada da baxılır. Həndəsi qurmalar üçün işlədilən klassik alətlər pərgar və xətkeşdir (bölgüsü olmayan birtərəfli xətkeş). Buna baxmayaraq, digər alətlərin köməyi ilə də həndəsi qurmalara baxılır. Məsələn, yalnız pərgarın köməyi ilə (Mor-Maskeroni qurmaları), müstəvi üzərində çevrə və onun mərkəzi verilibsə, təkcə, xətkeşin köməyi ilə (Şteyner qurmaları) qıraqları paralel olan ikitərəfli xətkeşlə, üçbucaq xətkeşlə (düzbucaqlı üçbucağın modeli) və s. alətlərin köməyi ilə həll edilən həndəsi qurmalar var. Müstəvi üzərində və fəzada bütün həndəsi qurmalar qurmanın postulatlarına (konstruktiv həndəsənin askiomları), yəni sadə, elementar qurmalara əsaslanır. Əgər verilmiş qurma məsələsi sonlu sayda elementar qurmalara gətirilirsə, bu qurma məsələsi həll olunmuş hesab olunur. Təbiidir ki, hər bir qurma alətinin özünün konstruktiv gücü var.

Tor (toroid) — doğuran çevrənin bu çevrə ilə eyni müstəvidə yerləşən və onu kəsməyən düz xəttin (fırlanma oxu) ətrafında firlanması nəticəsində alınan səth. Bəzən doğuran çevrənin fırlanma oxunu kəsməməsi də istisna olur. Belə olan halda, əgər doğuran çevrə fırlanma oxunu kəsərsə, yaxud ona toxunarsa, belə tor qapalı tor, əks halda açıq tor adlanır.

Fiqurativ təsvirlərdən yayınan İslam incəsənətində əsrlər boyu həndəsi naxışların təsvirindən istifadə edilmiş, bu incəsənət növü geniş yayılmış və inkişaf etmişdir. İslam incəsənətində həndəsi dizaynlar tez-tez təkrarlanan kvadratlar və dairələrin birləşmələri, islimilər, müxtəlif naxışlar və tessaliyaların təsvirindən ibarətdir. Bu təsvirlərdən bütün dekorasiyanı tərtib etmək, çiçək və ya xətt bəzəkləri üçün çərçivə və ya digər motivlər üçün arxa plan yaratmaq məqsədilə istifadə edilə bilər. İstifadə edilən bəzəklərin qarışıqlığı və müxtəlifliyi, IX əsrdə olan sadə ulduzlara və paxlava şəkilli təsvirlərə, XIII əsrdə 6 və 13 guşəli ulduzların, XVI əsrdə isə 14 və 16 guşəli ulduzların əlavə edilməsi nəticəsində yaradılmışdır. Həndəsi naxışlar İslam incəsənətində və memarlığında kilim xalçalar, İran girih və Mərakeş zillic işləri, muqarna dekorativ tağları, cali oyulmuş daş lövhələri, keramikalar,dəri, rəngli şüşələr, ağac və metal işləri ilə əhatələnmişdir. XX əsrdə qərbdə, aralarında M.K.Eşerin də olduğu ustalar, rəssamlar və 2007-ci ildə İsfahandakı Darbe-İmam məqbərəsində olan yarı-dövri funksiyaları və penroz bəzəklərini də bu üsluba daxil edən riyaziyyatçılar və fiziklər (Peter J. Lu və Paul Steynhardın aralarında olduğu) arasında İslam həndəsi nümunələrinə olan maraq artmaqda idi. İslam incəsənəti əsasən ibadət obyekti ola biləcəyini önləmək üçün təsvirlərdə fiqurativ simvollardan yayınmışdır. İslam həndəsi nümunələri qədim mədəniyyətlərdə istifadə edilən daha sadə dizayn nümunələrindən təsirlənmişdir. Bunlara yunan, roma və sasani mədəniyyətlərini nümunə kimi göstərmək olar. Bunlar İslam incəsənət nümunələrinin üç əsas formalarından biridir: digərləri isə, əyilmiş və budaqlı bitki təsvirləri ilə formalaşdırılan islimi və İslam xəttatlığıdır.

Fiqurativ təsvirlərdən yayınan İslam incəsənətində əsrlər boyu həndəsi naxışların təsvirindən istifadə edilmiş, bu incəsənət növü geniş yayılmış və inkişaf etmişdir. İslam incəsənətində həndəsi dizaynlar tez-tez təkrarlanan kvadratlar və dairələrin birləşmələri, islimilər, müxtəlif naxışlar və tessaliyaların təsvirindən ibarətdir. Bu təsvirlərdən bütün dekorasiyanı tərtib etmək, çiçək və ya xətt bəzəkləri üçün çərçivə və ya digər motivlər üçün arxa plan yaratmaq məqsədilə istifadə edilə bilər. İstifadə edilən bəzəklərin qarışıqlığı və müxtəlifliyi, IX əsrdə olan sadə ulduzlara və paxlava şəkilli təsvirlərə, XIII əsrdə 6 və 13 guşəli ulduzların, XVI əsrdə isə 14 və 16 guşəli ulduzların əlavə edilməsi nəticəsində yaradılmışdır. Həndəsi naxışlar İslam incəsənətində və memarlığında kilim xalçalar, İran girih və Mərakeş zillic işləri, muqarna dekorativ tağları, cali oyulmuş daş lövhələri, keramikalar,dəri, rəngli şüşələr, ağac və metal işləri ilə əhatələnmişdir. XX əsrdə qərbdə, aralarında M.K.Eşerin də olduğu ustalar, rəssamlar və 2007-ci ildə İsfahandakı Darbe-İmam məqbərəsində olan yarı-dövri funksiyaları və penroz bəzəklərini də bu üsluba daxil edən riyaziyyatçılar və fiziklər (Peter J. Lu və Paul Steynhardın aralarında olduğu) arasında İslam həndəsi nümunələrinə olan maraq artmaqda idi. İslam incəsənəti əsasən ibadət obyekti ola biləcəyini önləmək üçün təsvirlərdə fiqurativ simvollardan yayınmışdır. İslam həndəsi nümunələri qədim mədəniyyətlərdə istifadə edilən daha sadə dizayn nümunələrindən təsirlənmişdir. Bunlara yunan, roma və sasani mədəniyyətlərini nümunə kimi göstərmək olar. Bunlar İslam incəsənət nümunələrinin üç əsas formalarından biridir: digərləri isə, əyilmiş və budaqlı bitki təsvirləri ilə formalaşdırılan islimi və İslam xəttatlığıdır.